[Machine Learning] 다중 선형 회귀(Multiple Linear Regression)

※ [Machine Learning] 회귀(Regression) 공부하기

[Machine Learning] 회귀(Regression)

저번 포스팅에서 한 개의 독립 변수(Independent Variable)에 기반한 회귀 분석 기법인 SLR를 배웠다. MLR은 이와 비슷한 회귀 분석 기법으로 둘 이상의 독립 변수에 기반한 선형 회귀를 지칭한다.

---

※ 참고

$n$	특성의 개수(Number of features)
$w_0$	편향(Bias)
$w_1, ..., w_n$	가중치(Weight)
$x_1, ..., x_n$	특성(Feature)

---

• 가설 공간(Hypothesis Space): 다음과 같은 형태의 함수 $h_{\mathbf {w}}: \mathbb {R}^{n + 1} \rightarrow \mathbb {R}$의 집합$$h_{\mathbf {w}}(\mathbf {x}) = w_0 + w_1 x_1 + w_2 x_2 +... + w_n x_n$$

※ 가중치와 편향을 결합해 $\mathbf {w}$라고 한다. 이에 맞게 $\mathbf {x}$도 편향을 고려해 $1$을 덧붙인다. 즉,

$$w = (w_0, w_1,..., w_n) $$

$$x = (1, x_1,..., x_n) \in \mathbb {R}^{n + 1}$$$$h_{\mathbf {w}}(\mathbf {x}) = \mathbf {w}^{\top} \mathbf {x}$$

---

선형 기저 함수 모델(Linear Basis Function Models)

※ 참고

$n$	특성의 개수(Number of features)
$k$	기저 함수의 개수(Number of basis functions)
$x = (x_1, ..., x_n)$	특성 벡터(Feature Vector)
$w = (w_0, ..., w_k)$	모수 벡터(Parameter Vector)
$\phi = (\phi_0, ..., \phi_k)$	기저 함수 벡터(Vector of Basis Functions)
$\phi_j: \mathbb {R}^n \rightarrow \mathbb{R}$	j번째 기저 함수(jth Basis Function)
$\phi_0(x) \equiv 1$	더미 기저 함수(Dummy Basis Function)

---

• 가설 공간 $\mathcal {H}_k$: 다음과 같은 형태의 함수 $h_{\mathbf {w}}: \mathbb {R}^{n} \rightarrow \mathbb {R}$의 집합$$h_{\mathbf {w}}(\mathbf {x}) = w_0 \phi_0(x) + w_1 \phi_1(x) + w_2 \phi_2(x) +... + w_k \phi_k(x) = \mathbf {w}^{\top} \phi (x)$$
• 선형 기저 함수 $h_{\mathbf {w}} (\mathbf {x})$는 선형적이더라도 선형 기저 함수를 구성하는 기저 함수 $\phi_j$는 비선형적일 수도 있다.
• 기저 함수 $\phi$의 예시) 정사영 함수, 전처리 함수, 다항 기저 함수, 방사형 기저 함수, 로지스틱 기저 함수 등.

※ $k$개의 기저 함수는 어떻게 모델을 설계하느냐에 따라 다르게 설정한다.

※ $\mathcal {H}_0 \subsetneq \mathcal {H}_1 \subsetneq \mathcal {H}_2 \subsetneq \mathcal \cdots \subsetneq \mathcal {H}_k$

---

예 1) 정사영 함수를 기저 함수로

• 기저 함수 $\phi_j: \mathbb {R}^n \rightarrow \mathbb {R}, \mathbf {x} \mapsto x_j \text { for all } j \in \{ 1, ..., n \}$
• 가설 공간 $\mathcal {H}$: $$\begin{align*} h_{\mathbf {w}}(\mathbf {x}) &= w_0 + w_1 \phi_1(x) + w_2 \phi_2(x) +... + w_n \phi_n(x) \\ &= w_0 + w_1 x_1 + w_2 x_2+... + w_n x_n \end{align*}$$

  ---

예 2) 전처리 함수를 기저 함수로

• 기저 함수 $$\phi_j(x) = \frac {x_j - \mu_j}{\sigma_j} \text { for all } j \in \{ 1, ..., n \}$$ $$\text {where } \mu_j = \frac {1}{m} \sum^{m}_{i = 1} x_{ij} \text { and } \sigma_j = \sqrt {\frac {1}{m - 1} \sum^{m}_{i = 1} (x_{ij}- \mu_j)^2}$$ $$\text {are the mean and standard deviation of the j-th feature over training data.}$$
• 주로 분류 작업에서 많이 전처리 함수를 기저 함수로 삼으며, 데이터를 표준화(Standardization)하는 효과가 있다.

Q. 데이터를 표준화한 특성은 무슨 의미이며, 어떤 경우에서 유용하게 사용될까?
A. 데이터가 가중치에 대해서 서로 다른 정도로 예민하게 반응한다면, 경사 하강법에서의 수렴에서 진동(Oscillation)하는 현상이 관찰될 수 있다. 따라서 이를 보완하기 위해 작은 합습률(Learning Rate) $\eta$를 사용해야 하는데, 이는 곧 느린 수렴(Slow Convergence)을 의미한다. 해당 문제를 해결하기 위해 데이터를 평균값과 분산에 대해서 정규화 혹은 표준화하는 방법이 있다. 정규화된 데이터를 실제 데이터 대신 사용하면 더 효율적으로 경사 하강법을 적용할 수 있으며, 학습률을 줄이지 않고 빠르게 수렴하도록 한다.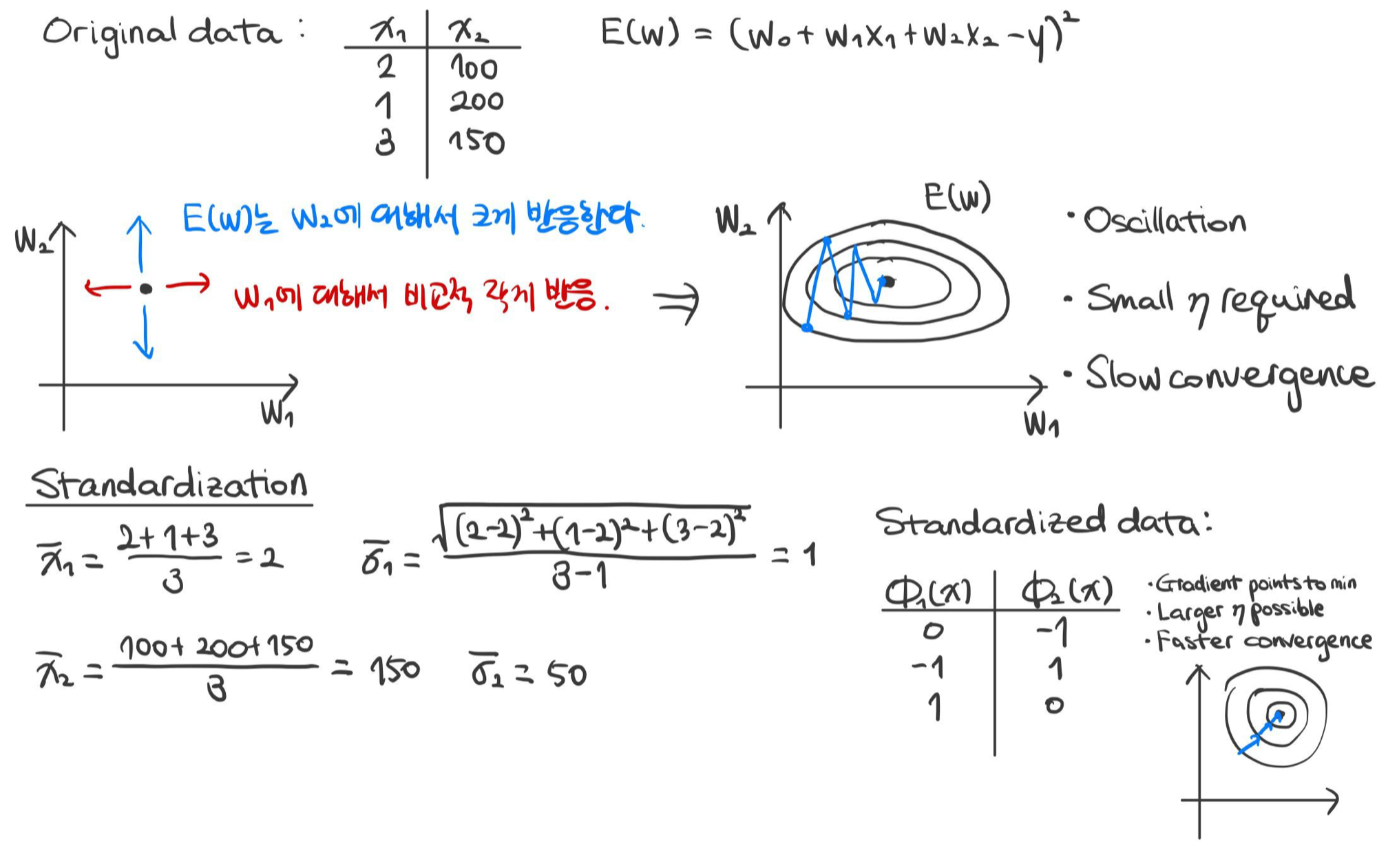

데이터의 표준화의 중요성

---

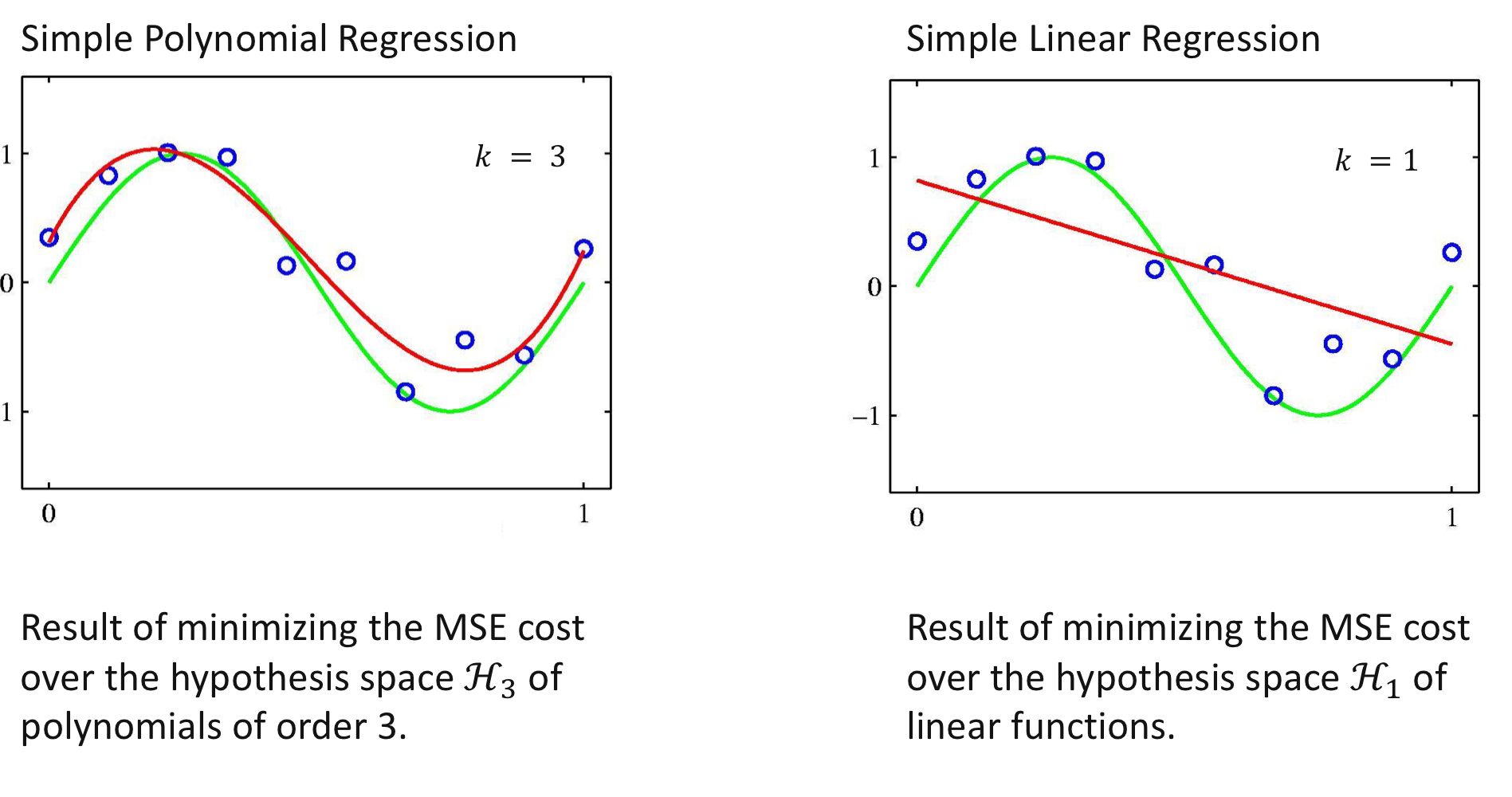
예 3) 다항 함수를 기저 함수로

• 기저 함수 ($n = 1$) $$\phi_j: \mathbb {R} \rightarrow \mathbb{R}, x \mapsto x^j$$
• 가설 공간 $\mathcal {H}_k$은 최고차항이 $k$인 다항 함수의 집합 $$\mathcal {H}_k = {h_{\mathbf {w}}(x) = w_0 + w_1 x + w_2 x^2 + ... + w_k x^k}$$

예 4) 방사형 함수를 기저 함수로

※ 참고

$\mu_j$	가우시안 분포의 중심(Centroid of Bell)
$\sigma_j$	가우시안 분포의 폭(Width of Bell)
$w_j$	가우시안 분포의 넓이(Amplitude of Bell)

• 가우시안 기저 함수(Gaussian Basis Function) $$\phi_j: \mathbb {R}^n \rightarrow \mathbb{R}, \mathbf {x} \mapsto \exp \left (- \frac {|| \mathbf {x} - \mu_j ||^2}{\sigma_j} \right )$$
• 가설 공간 $\mathcal {H}_k$: 다음과 같은 형태의 함수 의 집합 $$h_{\mathbf {w}}(\mathbf {x}) = w_0 + w_1 \exp \left (- \frac {|| \mathbf {x} - \mu_1 ||^2}{\sigma_1} \right ) + w_2 \exp \left (- \frac {|| \mathbf {x} - \mu_2||^2}{\sigma_2} \right ) + ... + w_k \exp \left (- \frac {|| \mathbf {x} - \mu_k ||^2}{\sigma_k} \right )$$

---

※ [Machine Learning] 단순 선형 회귀(Simple Linear Regression)

[Machine Learning] 단순 선형 회귀(Simple Linear Regression)

※ [Machine Learning] 경사 하강법(Gradient Descent)

[Machine Learning] 경사 하강법(Gradient Descent)

---

MLP의 ERM과 경사 하강법

가정

학습 데이터 세트(Training Dataset)$(\mathbf {x}_1, y_1), (\mathbf {x}_2, y_2), ..., (\mathbf {x}_m, y_m) \in \mathbb {R}^{n} \times \mathbb {R}$를 가정하자. 가설 공간은 다음 형태의 함수의 집합을 이룬다. $h_{\mathbf {w}}(\mathbf {x}) = w_0 \phi_0(\mathbf {x}) + w_1 \phi_1(\mathbf {x}) + ... + w_k \phi_k(\mathbf {x}) = \mathbf {w}^{\top} \phi(\mathbf {x})$

---

목표

ERM 기법으로 다음 MSE를 최소화하여라.

$$J(\mathbf {w}) = \frac {1}{2m} \sum^{m}_{i = 1} (h_{\mathbf {w}}(\mathbf {x}_i) - y_i)^2 = \frac {1}{2m} (\Phi \mathbf {w} - \mathbf {Y})^{\top} (\Phi \mathbf {w} - \mathbf {Y})$$

※ 참고 $$\Phi = \begin {pmatrix} \phi_0(\mathbf {x}_1) & \phi_1(\mathbf {x}_1) & \dots & \phi_k(\mathbf {x}_1) \\ \phi_0(\mathbf {x}_2) & \phi_1(\mathbf {x}_2) & \dots & \phi_k(\mathbf {x}_2) \\ \dots & \dots & \dots & \dots \\ \phi_0(\mathbf {x}_m) & \phi_1(\mathbf {x}_m) & \dots & \phi_k(\mathbf {x}_m)\end {pmatrix} $$

미분으로 최적의 $\mathbf {w}$ 구하기

$$\mathbf {w} = (\Phi^{\top} \Phi)^{-1} \Phi^{\top} \mathbf {Y} \ \ \ \text {if } \Phi^{\top} \Phi \text { is non-singular}$$

경사 하강법 적용

$$w_j \rightarrow w_j - \eta \frac {\partial}{\partial w_j} J(\mathbf {w}) \ \ \ \text {for all } j$$ $$\therefore \mathbf {w} \rightarrow \mathbf {w} - \frac {\eta}{m} \Phi^{\top} (\Phi \mathbf {w} - \mathbf {Y})$$

---

1. Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification (2nd Edition). Wiley-Interscience, USA.

2. Müller, K.R., Montavon, G. (2021). Lecture on Machine Learning 1-X. Technische Universität Berlin, Berlin, Germany.