[Machine Learning] 최대우도법(Maximum Likelihood Estimation)

최대우도법은 어떤 확률 변수(Random Variable)에서 표집한 값들을 토대로 그 확률 변수의 모수(Parameter)를 구하는 방법이다. 어떤 모수가 주어졌을 때, 원하는 값들이 나올 우도(Likelihood)를 최대로 만드는 모수를 선택한다. [wikipedia]

---

평균(Mean)이나 공분산(Covariance)으로 이루어진 모수 벡터(Parameter Vector) $\theta$와 데이터에 대한 확률 밀도 함수(Probability Density Function) $p(\mathbf{x}|\theta )$를 가정할 때, 데이터를 가장 잘 모델링할 수 있는, 즉, 최대 우도를 갖는 모수 $\theta$들을 찾고자 한다.

• 데이터 세트(Dataset) $\mathcal{D}=({\mathbf{x}}_1,...,{\mathbf{x}}_N)$
• 데이터의 각 예시 ${\mathbf{x}}_k\in {\mathbb{R}}^d$는 독립적으로 같은 밀도 함수 $p(\mathbf{x}|\theta )$에 의해 생성한다.
• 결합 확률 밀도 함수(Joint Density Function)는 다음과 같다. $$p(\mathcal{D}|\theta )=\prod _{k=1}^{N}p({\mathbf{x}}_k|\theta )$$. 이를 데이터 세트 $\mathcal{D}$에 대하여 $\theta$의 우도라고 한다.
• $\mathcal{D}$에 대하여 $\theta$의 우도가 가장 큰 $\theta$를 선택한다. $\hat{\theta }=arg\underset{\theta }{max}p(\mathcal{D}|\theta )$

※ 편리성을 위해, $p(\mathcal{D}|\theta )=\prod _{k=1}^{N}p({\mathbf{x}}_k|\theta )$ 대신 로그 우도(Log-Likelihood) $\log p(\mathcal{D}|\theta )=\sum _{k=1}^N\log p({\mathbf{x}}_k|\theta )$를 구한다.

Q. 우도 대신 로그 우도를 대신 구하는 이유는?
A. $p({\mathbf{x}}_k|\theta )$는 모수에 대한 데이터의 가능성을 나타내기 때문에 작은 값을 가질 확률이 높다. $p(\mathcal{D}|\theta )$를 구하기 위해 $p({\mathbf{x}}_k|\theta )$를 모두 곱하면, 매우 작은 값을 갖게 되어 컴퓨터에서의 계산이 어려울 수가 있다. 따라서 단조 증가함수(Monotonically Increasing Function)인 로그 함수(Log Function)를 적용하여 결괏값에 영향을 끼치지 않고 수월하게 MLE을 구할 수 있다.

따라서 최적의 모수를 찾는 MLE는 다음의 식과 같다.

$$\hat{\theta }=arg\underset{\theta }{max}\log p(\mathcal{D}|\theta )=arg\underset{\theta }{max}\sum _{k=1}^N\log p({\mathbf{x}}_k|\theta )$$

---

예시 1) 오류가 가우시안 분포(Gaussian Distribution)를 따를 때($y=f(\mathbf{x})+ϵ,ϵ\sim \mathcal{N}(0,{\sigma }^2)$)

위의 모델 $y$에 대한 사후 확률(Posterior Probability)은 $p(y|\mathbf{x},f,{\sigma }^2)$으로 $\mathcal{N}(y|f(\mathbf{x}),{\sigma }^2)$ 분포를 갖는다.

학습 예시 $({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),...,({\mathbf{x}}_m,y_m)\in {\mathbb{R}}^m\times \mathbb{R}$가 $P(\mathbf{x},y)=p(y|\mathbf{x})P(\mathbf{x})$로부터 독립적으로 생성된다고 가정하자.

위의 그림에서 MLE로 최적의 가설을 찾는 것은 MSE를 최소화하는 것과 같음을 증명한다.

---

예시 2) 정규 분포($\mathbf{x}\sim \mathcal{N}(\theta ,1)$)

해당 모델의 데이터 ${\mathbf{x}}_k$의 밀도 함수는 다음과 같이 쓸 수 있다.

$$p({\mathbf{x}}_k|\theta )=\frac{1}{\sqrt{2\pi }}\exp (-\frac{1}{2}(x_k-\theta {)}^2)$$

모든 데이터들이 독립적으로 생성되었다는 가정하에 결합 우도와 로그 우도는 다음과 같다.

$$\begin{array}{rl}p(\mathcal{D}|\theta )& =\prod _{k=1}^N\frac{1}{\sqrt{2\pi }}\exp (-\frac{1}{2}(x_k-\theta {)}^2)\\ \log p(\mathcal{D}|\theta )& =\sum _{k=1}^N[-\frac{1}{2}\log 2\pi -\frac{1}{2}(x_k-\theta {)}^2]\end{array}$$

---

예시 3) 다변량 정규분포(Multivariate Normal Distribution) ($\mathbf{x}\sim \mathcal{N}(\mu ,\mathrm{\Sigma })$)

다변량 정규분포의 확률 밀도 함수(Multivariate Normal Distribution pdf):
$$p(\mathbf{x}|w_i)=\frac{1}{\sqrt{(2\pi {)}^{d}det({\mathrm{\Sigma }}_i)}}\exp (-\frac{1}{2}(\mathbf{x}-{\mu }_i{)}^{\mathrm{\top }}{\mathrm{\Sigma }}_i^{-1}(\mathbf{x}-{\mu }_i))$$

다변량 정규분포의 평균값 추정

다변량 정규분포의 공분산 추정

---

예시 4) 베루누이 분포(Bernoulli Distribution)

데이터 $x_1,...,x_m$이 성공률(Success Probability) $p$를 갖는 베르누이 분포를 따를 때, MLE로 $\hat{p}$를 구하여라.

---

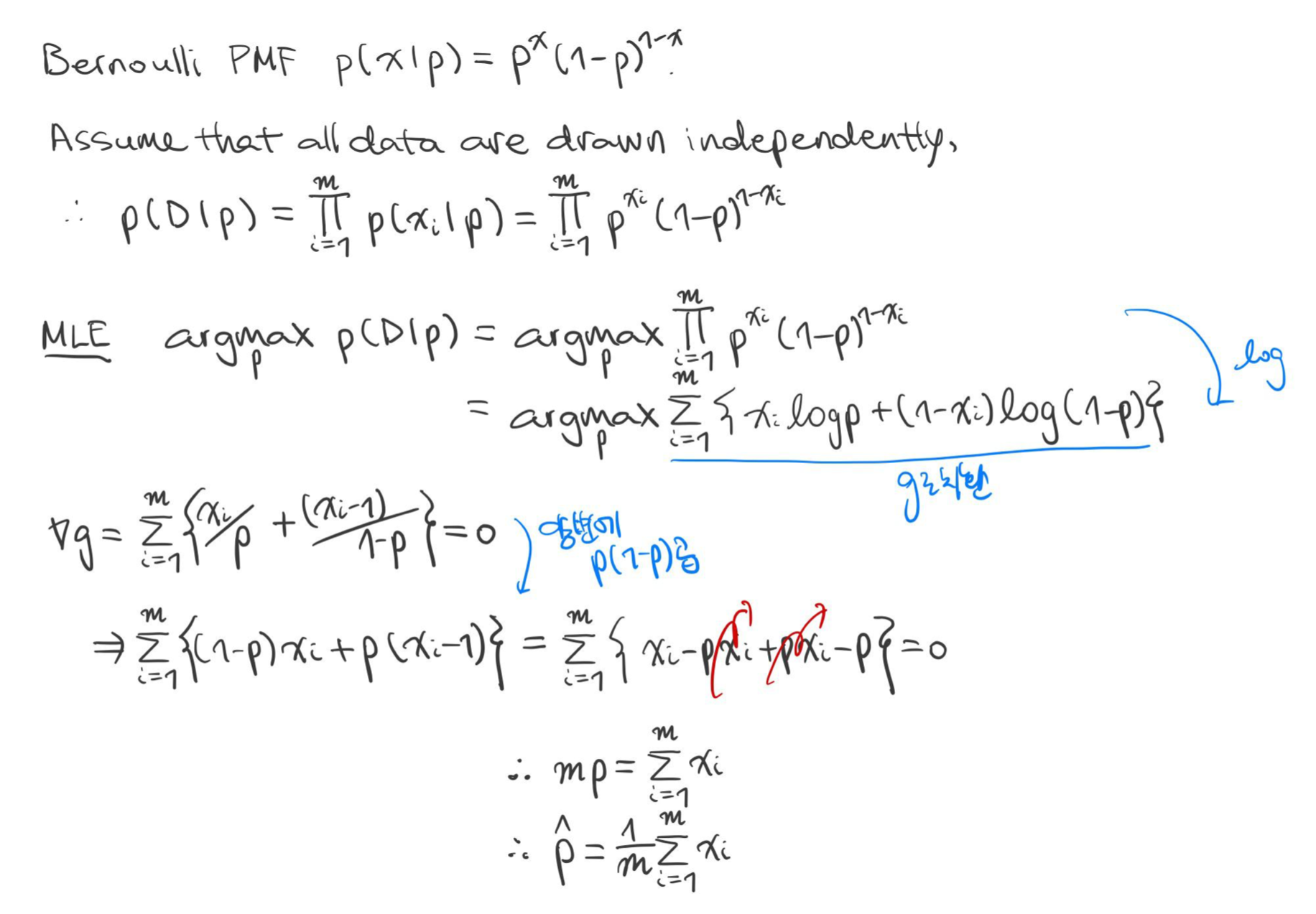
예시 5) $p(x,y)=\lambda \eta {\exp }^{-\lambda x-\eta y},(\lambda ,\eta >0)$

위의 확률 분포를 따르는 데이터 세트 $\mathcal{D}=\{(x_1,y_1),...,(x_N,y_N)\}$가 있다고 가정하자.

---

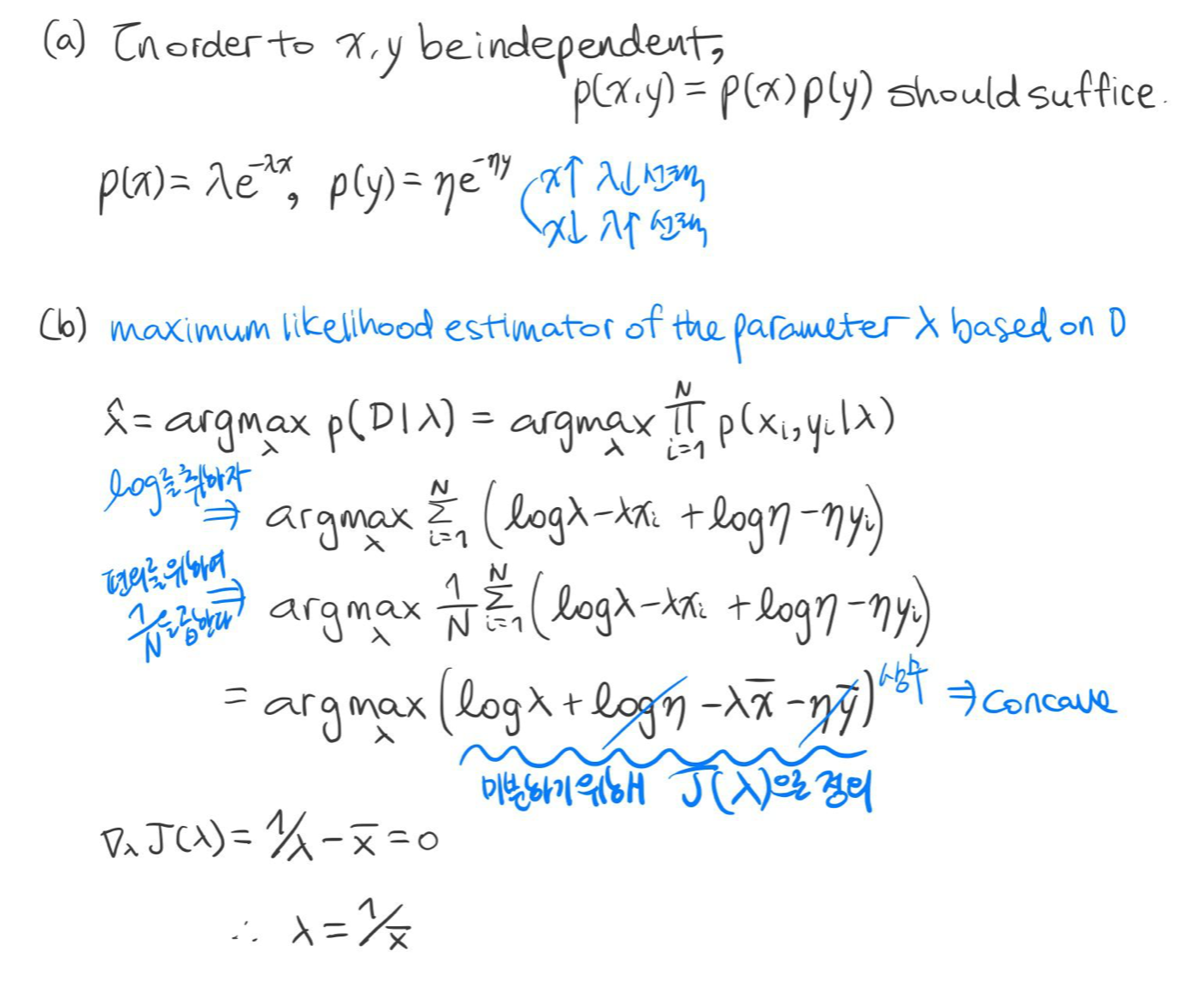
예 6) 기하 분포(Geometric Distribution)

아래의 그림은 기하 분포를 따르는 데이터를 두 클래스 $w_1$와 $w_2$로 분류하고자 하는 예를 보여준다. 각각 클래스를 50 % 확률로 분류할 수 있으며 알려지지 않은 모수 $\theta$와 그에 대한 확률 분포 $P(x=k|\theta )=(1-\theta {)}^k\theta$로 데이터 세트 ${\mathcal{D}}_1$와 ${\mathcal{D}}_2$로 분류된다.

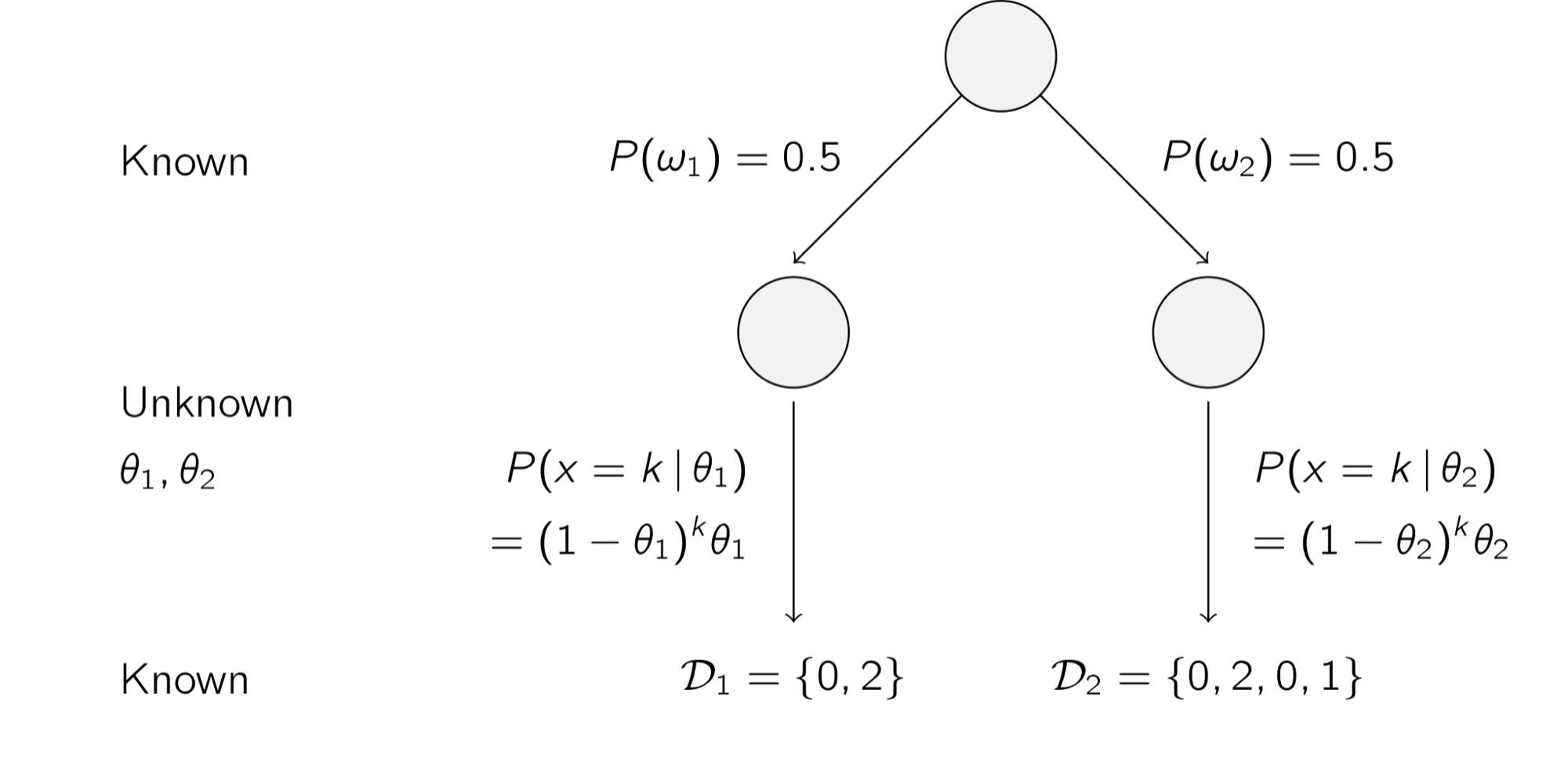
k = 1일 때의 분류기 예시

이처럼 MLE를 이용해 알려지지 않은 확률 분포 모수를 예측할 수 있으며, 예측한 모수에 베이즈 이론을 적용해 데이터를 분류한다.