-
[Machine Learning] 베이즈 결정 이론(Bayesian Decision Theory)Informatik 2022. 1. 14. 19:01
지도 학습(Supervised Learning)의 분류(Classification)에 해당하는 머신러닝(Machine Learning) 기법인 베이즈 결정 이론은 일상생활에서 흔하게 볼 수 있고 사용할 수 있는 기법이다. 예를 들어, 스팸 메일을 분류할 때 사용하거나, 가짜 뉴스를 판별한다던지, 더 나아가서 숫자, 글자, 문서까지도 분류할 수 있다.
베이즈 결정 이론의 큰 범주로 예 / 아니오로 분류하는 이진 분류(Binary Classification)와 여러 개의 군으로 분류하는 멀티 클래스 분류(Mutli-Class Classification)로 나눌 수 있다. 앞에서 든 예로 스팸 메일 분류와 가짜 뉴스 판별은 이진 분류에 해당하고, 숫자, 글자, 문서 분류는 멀티 클래스 분류에 해당한다.
이진 분류(Binary Classification)

머신러닝의 교과서 Duda의 예시를 빌려서, 어떤 생선 공장에서 농어와 연어를 구별하는데 머신러닝을 적용한다고 가정해보자. 카메라 센서를 달아서 각 생선의 길이를 측정하는데, 그 길이에 따라서 농어와 연어를 분별하고자 한다. 기본 원칙은 다음과 같다:
생선 길이 관찰 → 생선 길이가 주어졌을 때 각 클래스에 속할 확률 계산→ 그 확률이 최대인 클래스로 분류
즉, 농어군 $w_1$, 연어군 $w_2$이라고 하고 측정한 모든 생선의 길이 $\mathbf {x} \in \mathbb {R}^d$라고 할 때, 생선 길이가 주어졌을 때 해당 클래스에 속할 확률인 사후 확률(Posterior Probability) $P(w_i | \mathbf{x})$를 계산한다. 그다음 $P(w_1 | \mathbf {x}) > P(w_2 | \mathbf {x})$이면 농어로 분류, $P(w_1 | \mathbf {x}) \leq P(w_2 | \mathbf {x})$이면 연어로 분류한다. 이와 같은 방법을 MAP(Maximum A Posteriori)라고 한다.
여기서 문제는 현실에서는 사후 확률을 직접 알 수 없는데 이를 유도하기 위해 베이즈 정리를 이용한다.
베이즈 이론 (Bayes Theory):
$$P(A | B) = \frac{P(B | A) P(A)}{P(B)}$$
베이즈 이론에 의하면 사후 확률 $P(w_i | \mathbf {x})$은 다음과 같이 나타낼 수 있다. $$P(w_i | \mathbf {x}) = \frac {p(\mathbf {x} | w_i) P(w_i)}{p(\mathbf {x})}$$.다시 말해서, 바로 구하지 못하는 사후 확률은 다음과 같이$$Posterior = \frac {Likelihood \times Prior}{Evidence}$$로 대신 계산한다. 베이즈 결정 이론에서 사용되는 확률들을 정리해보면 다음과 같다.
- 사후 확률(Posterior Probability) $P(w_i | \mathbf {x})$: 결정적으로 구해야 하는 요소.
- 우도(Likelihood) $p(\mathbf {x} | w_i)$: 각 분류에 대해서 생선 길이가 관찰될 밀도 함수.
- 사전 확률(Prior Probability) $P(w_i)$: 미리 알고 있는 각 분류에 대한 발생 확률.
- 증거(Evidence) $p(\mathbf {x})$: 생선 길이에 대한 밀도 함수. 정규화된 상수로 베이즈 결정 이론에서는 결정에 영향을 끼치지 않아 무시한다.
최적 결정 함수(Optimal Decision Function) MAP은 사후 확률이 최대가 되는 클래스를 일컬으며, 여기에 베이즈 이론을 적용하면 베이즈 최적 분류기(Bayes Optimal Classifier)는 다음과 같다.$$
\begin {align*}
arg \max_i P(w_i | \mathbf {x}) &= arg\max_i \left [ \frac{p(\mathbf {x} | w_i) P(w_i)}{p(\mathbf{x})} \right] \\
&= arg\max_i \left[ p(\mathbf{x} | w_i) P(w_i) \right]\\
&= arg\max_i \log \left [ p(\mathbf{x} | w_i) P(w_i) \right ] \\
&= arg\max_i \left [ \log p(\mathbf{x} | w_i) + \log P(w_i) \right ]
\end {align*}
$$
이진 분류의 손실 함수(Loss Function of Binary Classification)
손실 함수(Loss Function) $l(\hat {w}, w)$란 $w$ 클래스로 분류되어야 할 데이터가 $\hat {w}$ 클래스로 잘못 분류됐을 때 발생하는 비용을 말한다. 예를 들어, 실제 농어가 베이즈 결정 이론에 의해 연어로 분류되었을 때 발생하는 손실 값이 있다.
예 1) 제로-원 손실(Zero-One Loss)
분류에서 일반적으로 사용되는 제로-원 손실은 맞게 분류되었을 때는 무손실, 잘못 분류되었을 때 1만큼 손실 값을 갖는다.
$$l(\hat {w}, w) = \begin{cases} 1 & \hat{w} \neq w \\ 0 & \hat{w} = w \end{cases} \\ \ \ \ (\hat{w} \in \{1, 2\})$$
예 2) 비대칭 손실(Non-Symmetric Loss)
비대칭 손실에서는 잘못 분류되었을 때 한쪽 클래스가 더 큰 손실을 갖는다. 예로 들어, 농어로 분류되어야 할 생선이 연어로 분류되었을 때의 손실 값이 그 역의 경우보다 큰 경우 $l(\hat {연어}, 농어) > l(\hat {농어}, 연어)$가 있다.
예 3) 제곱 손실(Squared Loss or L2)
L2 함수는 실제 클래스와 예측된 클래스의 차이의 제곱으로 머신러닝에서 자주 사용되는 손실 함수 중에 하나지만 이상치(Outlier)에 취약하다는 단점이 있다. 하지만 이진 분류에서는 분류될 수 있는 클래스의 수가 두 가지이므로 손실 함수로 L2를 적용해도 괜찮다.
$$l(\hat {w}, w) = (\hat{w} - w)^2$$
조건부 손실 기댓값(Expected Conditional Loss)
농어나 숭어로 분류될 수 있는 어떤 생선이 $w_l$ 클래스로 예측되었다고 가정해보자. $w_l$ 클래스로 예측할 조건부 손실 기댓값 $L$은 각 경우에 대해서 손실 함수와 클래스에 대한 사후 확률을 곱하여 모두 더한 것과 같다.
$$L(w_l | \mathbf {x}) = l(w_l, w_1) P(w_1 | \mathbf{x}) + l(w_l, w_2) P(w_2 | \mathbf {x})$$
손실 기댓값(Expected Loss)
의사결정 규칙(Decision Rule)을 관찰 값 $\mathbf {x}$에 대해서 클래스 $w$로 분류하는 함수 $h(\mathbf {x}) = w$라고 할 때, 손실 기댓값은 다음과 같다.
$$\begin {align*}
L [h] &= \int L (h (\mathbf {x}), \mathbf {x}) d \mathbf {x} = \int L(h (\mathbf {x}) | \mathbf {x}) p(\mathbf {x}) d \mathbf {x}
\end {align*}$$where $h: \mathbb{R}^n \rightarrow \{1, 2\}$ is a decision rule.
따라서 이진 분류에서 손실 기댓값은 다음과 같이 정리한다.
$$
\begin {align*}
L [h] &= \int L(h(\mathbf {x}) | \mathbf{x}) p(\mathbf {x}) d\mathbf {x} \\
&= \int \left \{ l(w_l, w_1) P(w_1 | \mathbf{x}) + l(w_l, w_2) P(w_2 | \mathbf{x}) \right \} p(\mathbf{x}) d\mathbf{x}
\end {align*}
$$결론적으로 목표는 조건부 손실 기댓값을 최소화하는 의사결정 규칙 $L [f] = \min_h L [h]$을 찾아 이진 분류의 성능을 최대화하는 것이다. (※ 손실 기댓값을 직접 최소화하기엔 $arg \min$ 계산에 불필요한 상수들이 포함되어 있다.)
$$f(\mathbf {x}) \in arg\min_i L(w_i | \mathbf{x}) = arg\min_i \left \{ l(w_i, w_1) P(w_1 | \mathbf{x}) + l(w_i, w_2) P(w_2 | \mathbf{x}) \right \}$$
예 1) 일반적인 예시
민희가 중고차를 사려고 한다. 사기 전에 $\mathbf {x}$ 요소들을 관찰했을 때 차가 고장 났을 확률이 $P(\text {defect} | \mathbf {x}) = 0.1$, 고장이 나지 않았을 확률이 $P(\text{no defect} | \mathbf{x}) = 0.9$라고 하자. 중고차를 살지 말지 결정에 대해서 아래의 정보를 이용해 손실을 최소화하는 결정을 구하자.
$$
\begin {align*}
l(\text {buy} | \text{defect}) = 100.0 \\
l(\text{buy} | \text {no defect}) = -20.0 \\
l(\text {not buy} | \text{defect}) = 0.0 \\
l(\text{not buy} | \text{no defect}) = 0.0
\end {align*}
$$$$
\begin {align*}
L(\text {buy}) | \mathbf {x}) &= l(\text{buy}, \text{defect}) P(\text{defect} | \mathbf{x}) + l(\text{buy}, \text{no defect}) P(\text{no defect} | \mathbf{x}) \\
&= 100.0 \times 0.1 + (-20.0) \times 0.9 = -8 \\
L(\text {not buy}) | \mathbf {x}) &= l(\text{not buy}, \text{defect}) P(\text{defect} | \mathbf{x}) + l(\text{not buy}, \text{no defect}) P(\text{no defect} | \mathbf{x}) \\
&= 0
\end {align*}
$$차를 안 샀을 때보다 차를 샀을 때 손실이 더 작으므로 차를 사기를 결정한다.
예 2) 제로-원 손실(Zero-One Loss)
$$
\begin {align*}
f(\mathbf {x}) &\in arg\min_i \left \{ l(w_i, w_1) P(w_1 | \mathbf{x}) + l(w_i, w_2) P(w_2 | \mathbf{x}) \right \} \\
&= arg\min_i P(w_k | \mathbf{x}) \ \ (k \neq i) \\
&= arg\min_i \left \{ 1 - P(w_i | \mathbf{x}) \right \} \\
&= arg\max_i P(w_i | \mathbf{x}) \\
&= arg\max_i p(\mathbf {x} | w_i) P(w_i)
\end {align*}
$$사후 확률 $P(w_1 | \mathbf {x})$와 $P(w_2 | \mathbf {x})$, 손실 함수 $l(w_1, w_2) = 2, l(w_2, w_1) = 1, l(w_1, w_1) = l(w_2, w_2) = 0$를 가정했을 때 베이즈 결정의 의사결정 규칙을 구해보자.
- $i = 1$일 경우
$$
\begin {align*}
l(w_i, w_1) P(w_1 | \mathbf {x}) + l(w_i, w_2) P(w_2 | \mathbf{x}) &= l(w_1, w_1) P(w_1 | \mathbf{x}) + l(w_1, w_2) P(w_2 | \mathbf{x}) \\
&= 2 P(w_2 | \mathbf{x})
\end {align*}
$$- $i = 2$일 경우
$$
\begin {align*}
l(w_i, w_1) P(w_1 | \mathbf {x}) + l(w_i, w_2) P(w_2 | \mathbf{x}) &= l(w_2, w_1) P(w_1 | \mathbf{x}) + l(w_2, w_2) P(w_2 | \mathbf{x}) \\
&= P(w_1 | \mathbf{x}) \\
&= 1 - P(w_2 | \mathbf{x})
\end {align*}
$$손실 기댓값이 최소가 되는 $i$를 찾아야 하므로 $2 P(w_2 | \mathbf {x})$와 $1 - P(w_2 | \mathbf{x})$를 비교하여 값이 더 작은 값의 $i$를 선택한다.
$$2 P(w_2 | \mathbf{x}) - \{ 1 - P(w_2 | \mathbf{x}) \} = 3 P(w_2 | \mathbf{x}) -1$$
$$
\begin {align*}
i =
\begin {cases}
1 & P(w_2 | \mathbf {x}) \leq \frac {1}{3} \\
2 & P(w_2 | \mathbf{x}) > \frac{1}{3}
\end {cases}
\end {align*}
$$
데이터의 분포의 예시들(Examples of Data Distribution)
관찰 값에 대한 밀도 함수인 우도는 일반적인 확률 분포(Probability Distribution)를 가정할 수가 있다.
예 1) 다변량 정규분포(Multivariate Normal Distribution)
다변량 정규분포의 확률 밀도 함수(Multivariate Normal Distribution pdf):
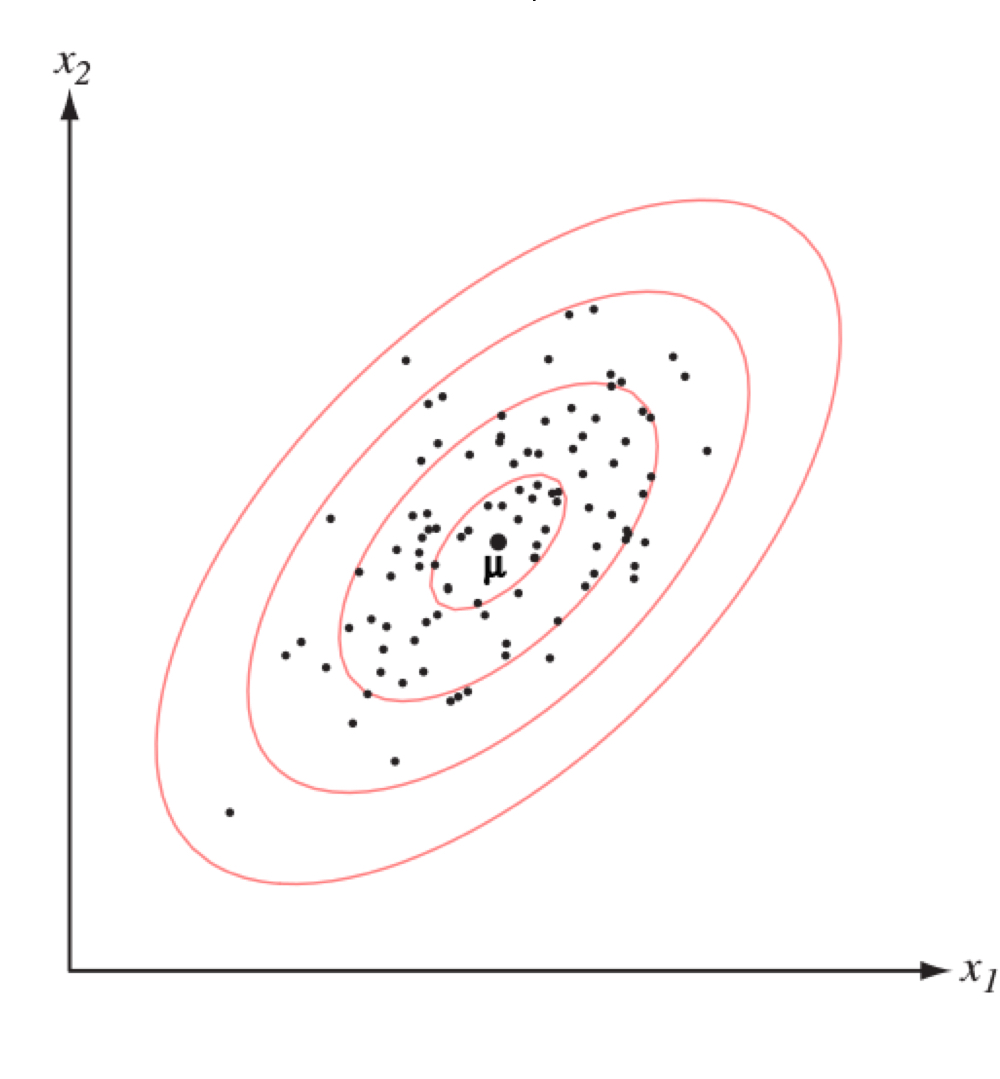
$$p(\mathbf {x} | w_i) = \frac{1}{\sqrt{(2 \pi)^d \det(\Sigma_i)}} \exp{\left (-\frac{1}{2} (\mathbf{x} - \mu_i)^{\top} \Sigma^{-1}_i (\mathbf{x} - \mu_i) \right )}$$- $\mu_i$: 평균값(Mean)으로, 데이터 분포의 중앙을 뜻한다.
- $\Sigma_i$: 공분산(Covariance)으로, 데이터 분포의 연장 및 차원 간의 상관관계를 뜻한다.
$$
\begin {align*}
arg \max_i P(w_i | \mathbf {x}) &= arg\max_i \left [ \log p(\mathbf {x} | w_i) + \log P(w_i) \right ] \\
&= arg\max_i \left [ \log \left \{ \frac {1}{\sqrt{(2 \pi)^d \det(\Sigma_i)}} \exp {\left (-\frac {1}{2} (\mathbf {x} - \mu_i)^{\top} \Sigma^{-1}_i (\mathbf{x} - \mu_i) \right )} \right \}+ \log P(w_i) \right ] \\
&= arg\max_i \left [ -\frac{1}{2} \log \left ( (2 \pi)^d \det(\Sigma_i) \right ) -\frac{1}{2} (\mathbf{x} - \mu_i)^{\top} \Sigma^{-1}_i (\mathbf{x} - \mu_i) + \log P(w_i) \right ] \\
&= arg\max_i \left [ -\frac {d}{2} \log (2 \pi) - \frac {1}{2} log \Sigma_i - \frac{1}{2} (\mathbf{x} - \mu_i)^{\top} \Sigma^{-1}_i (\mathbf{x} - \mu_i) + \log P(w_i) \right ] \\
&= arg\max_i \left [ - \frac{1}{2} (\mathbf{x} - \mu_i)^{\top} \Sigma^{-1}_i (\mathbf{x} - \mu_i) -\frac{d}{2} \log (2 \pi) - \frac{1}{2} log \Sigma_i + \log P(w_i) \right ] \\
&= arg\max_i \left [ - \frac {1}{2} \mathbf{x}^{\top} \Sigma^{-1}_i \mathbf{x} + \frac{1}{2} \mathbf{x}^{\top} \Sigma^{-1}_i \mu_i + \frac{1}{2} \mu_i^{\top} \Sigma^{-1}_i \mathbf{x} - \frac{1}{2} \mu_i^{\top} \Sigma^{-1}_i \mu_i \\
-\frac {d}{2} \log (2 \pi) - \frac {1}{2} log \Sigma_i + \log P(w_i) \right ] \\ &= arg\max_i \left [\frac{1}{2} \mathbf{x}^{\top} \Sigma^{-1}_i \mu_i + \frac{1}{2} \mu_i^{\top} \Sigma^{-1}_i \mathbf{x} - \frac{1}{2} \mu_i^{\top} \Sigma^{-1}_i \mu_i - \frac{1}{2} log \Sigma_i + \log P(w_i) \right ] \\
&= arg\max_i \left [\mathbf {x}^{\top} \Sigma^{-1}_i \mu_i + \left ( - \frac {1}{2} \mu_i^{\top} \Sigma^{-1}_i \mu_i - \frac{1}{2} log \Sigma_i + \log P(w_i) \right ) \right ]
\end {align*}
$$
예 1-a) 평균값이 다르고, 공분산이 같을 때 ($\mu_1 \neq \mu_2, \Sigma_1 = \Sigma_2$)
$$
\begin {align*}
arg \max_i P(w_i | \mathbf {x}) &= arg\max_i \left [\mathbf {x}^{\top} \Sigma^{-1}_i \mu_i + \left ( - \frac {1}{2} \mu_i^{\top} \Sigma^{-1}_i \mu_i - \frac{1}{2} log \Sigma_i + \log P(w_i) \right ) \right ] \\
&= arg\max_i \left [\mathbf{x}^{\top} \Sigma^{-1} \mu_i + \left ( - \frac{1}{2} \mu_i^{\top} \Sigma^{-1} \mu_i + \log P(w_i) \right ) \right ] \\
&= arg\max_i [v_i + b_i]
\end {align*}
$$마지막 줄에서는 간편성을 위해 $\mathbf {x}$에 대한 $v_i$와 $\mathbf{x}$ 독립적인 $b_i$로 치환했다.
일변량 정규분포의 확률 밀도 함수(Univariate Normal Distribution pdf):
$$p(\mathbf {x} | w_i) = \frac {1}{\sigma_i \sqrt {2 \pi}} \exp \left ( - \frac{(x - \mu_i)^2}{2 \sigma_i^2} \right )$$
공분산이 같을 때 다변량 정규분포 확률 밀도 함수(Multivariate Normal Distribution pdf):
$$p(\mathbf {x} | w_i) = \frac{1}{\sqrt{(2 \pi)^d \det(\Sigma)}} \exp{\left (-\frac{1}{2} (\mathbf{x} - \mu_i)^{\top} \Sigma^{-1} (\mathbf{x} - \mu_i) \right )}$$
아래의 그림은 다변량 정규분포에서 평균값이 다르고 공분산이 같아 두 개의 다차원 상의 정규분포(Normal Distribution) 혹은 가우시안 분포(Gaussian Distribution)를 띄게 되는 데이터 분포 그래프를 보여준다.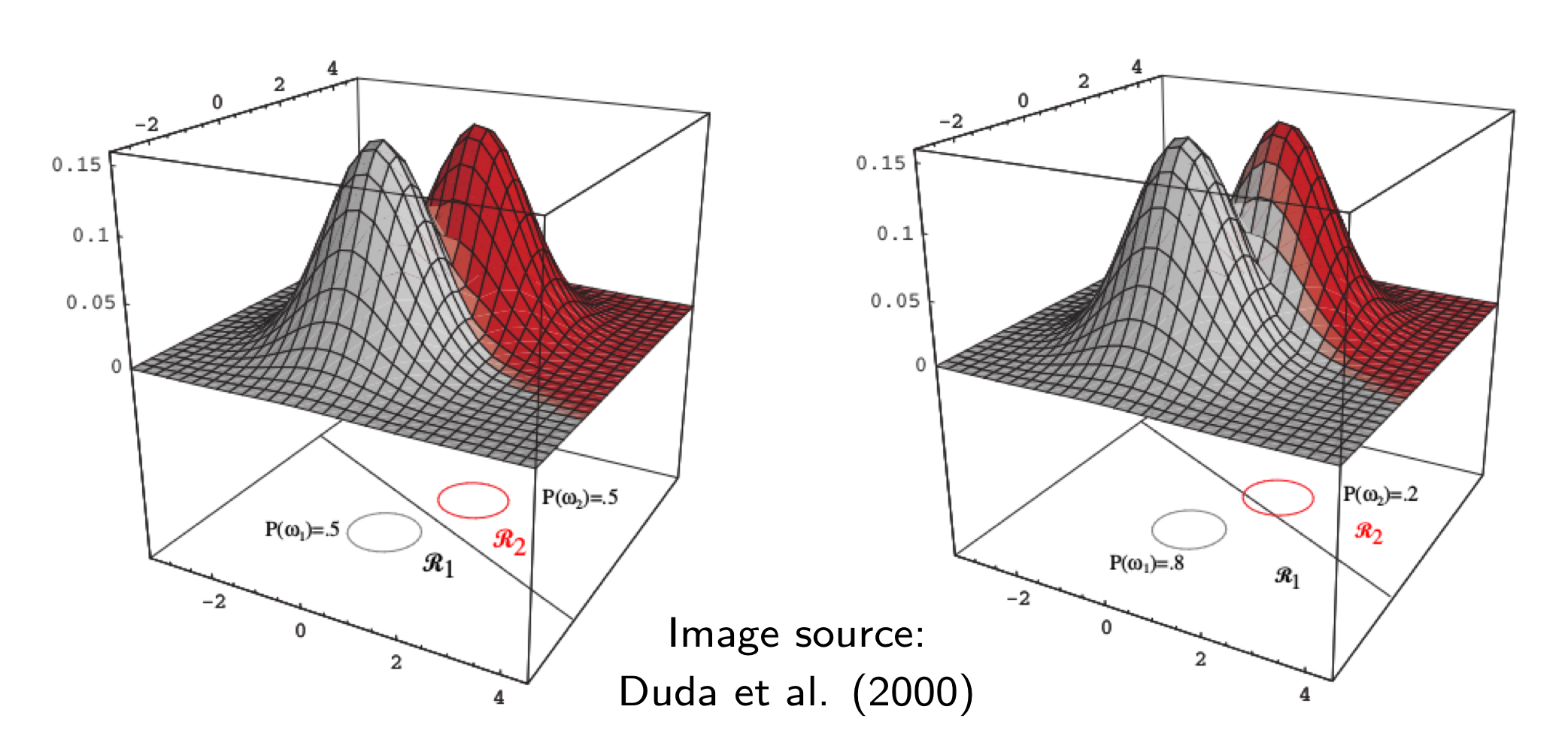
베이즈 결정 이론의 MAP으로 분류된 클래스를 그래프 선상으로 표현했을 때 위의 그림처럼 결정 경계(Decision Boundary)가 선형적인 것을 관찰할 수 있다. 위의 왼쪽 그림에서는 사전 확률이 같을 때($P(w_1) = P(w_2) = 0.5$)의 결정 경계를 보여준다. 이 경우, 두 가우시안 분포가 맞닺는 부분에서 선형적인 결정 경계가 형성된다. 반면, 위의 오른쪽 그림처럼 사전 확률이 다른 경우 ($P(w_1) = 0.8, P(w_2) = 0.2$)에는 선형적인 결정 경계가 형성되지만 사전 확률의 비율에 따라 그 경계가 한쪽으로 더 치우치게 된다.
예 1-b) 평균값이 같고, 공분산도 같을 때 ($\mu_1 = \mu_2, \Sigma_1 = \Sigma_2$)
$$
\begin {align*}
arg \max_i P(w_i | \mathbf {x}) &= arg\max_i \left [\mathbf {x}^{\top} \Sigma^{-1}_i \mu_i + \left ( - \frac {1}{2} \mu_i^{\top} \Sigma^{-1}_i \mu_i - \frac{1}{2} log \Sigma_i + \log P(w_i) \right ) \right ] \\
&= arg\max_i \left [\mathbf{x}^{\top} \Sigma^{-1} \mu - \frac{1}{2} \mu^{\top} \Sigma^{-1} \mu + \log P(w_i) \right ] \\
&= arg\max_i \log P(w_i)
\end {align*}
$$다변량 정규분포에서 평균값과 공분산이 모두 같으면 순전히 사전 확률 $P(w_i)$에 의해서 분류한다. 여기서 주의점은, 만약 $P(w_i)$가 모두 같은 값을 갖고 있다면 분류가 불가능해진다.
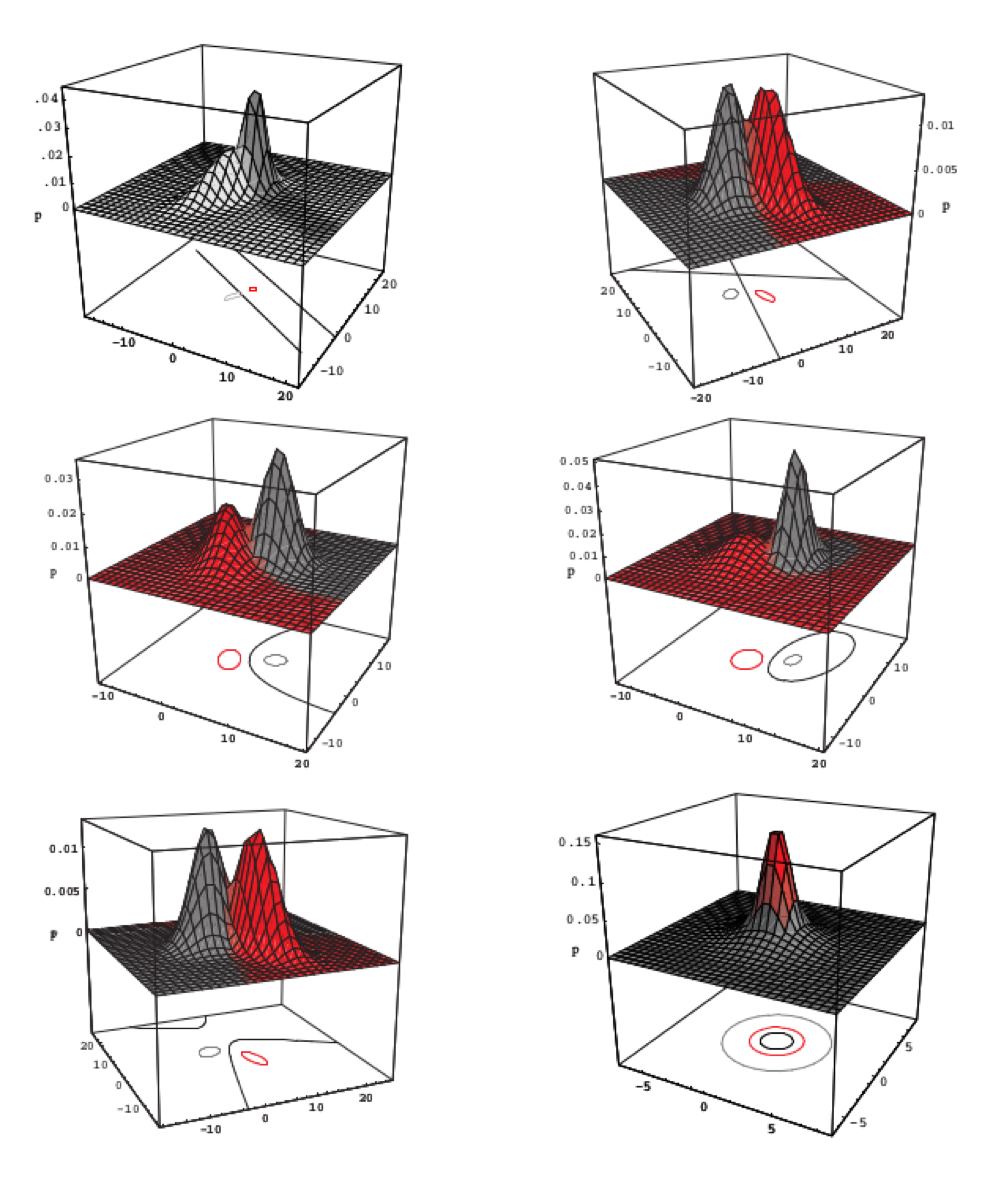
예 1-c) 공분산이 다를 때 ($\Sigma_1 \neq \Sigma_2$)
다변량 정규분포의 평균값과 무관하게 공분산이 다른 경우에는 2차 방정식 형태의 결정 경계를 갖는다.
예 2) 라플라스 분포(Laplace Distribution)
라플라스 분포의 확률 밀도 함수(Laplace Distribution pdf):
$$p(x | w_1) = \frac {1}{2 \sigma} \exp \left ( - \frac {|x - \mu|}{\sigma} \right ), p(x | w_2) = \frac{1}{2 \sigma} \exp \left ( - \frac{|x + \mu|}{\sigma} \right )$$ where $\mu, \sigma > 0$.
이진 분류의 오류 확률(Probability in Binary Classification)
이진 분류에서 생선의 길이가 관찰되었을 때 오류는 농어가 연어로 분류되었을 때 혹은 연어가 농어로 분류되었을 때, 두 가지 경우가 있다.
$$P(error | \mathbf {x}) = \begin{cases} P(w_1 | \mathbf{x}) & \text {if we decide}\ w = 2 \\ P(w_2 | \mathbf{x}) & \text{if we decide}\ w = 1 \end {cases}$$
따라서 오류를 최소화하기 위해서는 정확히 분류해야 하며 이는 베이즈 결정 규칙 MAP에 의하면 다음과 같다.
$$
\begin {align*}
\text {decide}\ w = 1 \text{ if } P(w_1 | \mathbf {x}) > P(w_2 | \mathbf{x}) \\
\text{decide}\ w = 2 \text{ if } P(w_1 | \mathbf{x}) \leq P(w_2 | \mathbf{x}) \\
\therefore P(error | \mathbf{x}) = \min {\{P(w_1 | \mathbf {x}), P(w_2 | \mathbf {x})\}}
\end {align*}
$$오류의 확률을 최소화하기 위해서는
$$P(error) = \int^\infty_{-\infty} P(error, \mathbf {x}) d\mathbf {x} = \int^\infty_{-\infty} P(error | \mathbf{x})p(\mathbf {x}) d\mathbf{x} = \int^\infty_{-\infty} \min{\{P(w_1 | \mathbf{x}), P(w_2 | \mathbf{x})\}} p(\mathbf{x}) d\mathbf {x}$$
로 계산할 수 있고 이를 베이즈 오류율(Bayes Error Rate)이라고 한다. 오류율은 $P(w_1 | \mathbf {x})$와 $P(w_2 | \mathbf{x})$ 둘 중 최솟값을 따르므로 $P(w_1 | \mathbf{x})$와 $P(w_2 | \mathbf{x})$의 차이가 크면 클수록 오류율이 작게 예측할 수 있다. 또, 베이즈 오류율은 $\min$ 함수가 적분 안에 있어 해석적으로 적분이 불가능하기 때문에 수치적 적분을 하거나 적분 값의 상한을 대신 구해야 한다.
베이즈 오류율의 상한(Upper Bound of Bayes Error Rate)
예 1) 가장 기본적인 상한
$P(w_2 | \mathbf{x}) = 1 - P(w_1 | \mathbf {x})$를 이용하면 다음과 같이 가장 기본적인 상한을 구할 수 있다.
$$
\begin {align*}
P(error) &= \int_\mathbf {x} \min{\{P(w_1 | \mathbf{x}), P(w_2 | \mathbf{x})\}} p(\mathbf {x}) d\mathbf {x} \\
&= \int_\mathbf{x} \min{\{P(w_1 | \mathbf{x}), 1 - P(w_1 | \mathbf{x})\}} p(\mathbf{x}) d\mathbf{x} \\
&\leq \int_\mathbf{x} 0.5 p(\mathbf{x}) d\mathbf{x} \\
&= 0.5
\end {align*}
$$이는 이진 분류에서 베이즈 오류율이 최대 50%, 정확도가 최소 50% 라는 것을 증명한다.
예 2) 베이즈 이론을 이용한 상한
$$
\begin {align*}
P(error) &= \int_\mathbf {x} \min {\{P(w_1 | \mathbf{x}), P(w_2 | \mathbf{x})\}} p(\mathbf{x}) d\mathbf{x} \\
&= \int_\mathbf {x} \min{\{P(w_1 | \mathbf{x})p(\mathbf{x}) , P(w_2 | \mathbf{x})p(\mathbf{x})\}} d\mathbf{x} \\
&= \int_\mathbf {x} \min {\{p(\mathbf{x} | w_1)P(w_1) , p(\mathbf{x} | w_2)P(w_2)\}} d\mathbf{x} \\
&\leq \int_\mathbf{x} \min{\{ \sum_i \{ p(\mathbf{x} | w_i) \} P(w_1), \sum_i \{ p(\mathbf{x} | w_i) \} P(w_2)\}} \\
&= \left (\sum_i \int_\mathbf{x} \sum_i \{ p(\mathbf{x} | w_i) \} d\mathbf{x} \right ) \cdot \min{\{ P(w_1), P(w_2)\}} \\
&= 2 \cdot 1 \cdot \min{\{ P(w_1), P(w_2)\}} \\
&= 2 \cdot \min{\{ P(w_1), P(w_2)\}}
\end {align*}
$$결론적으로 사전 확률이 불균등할수록 베이즈 오류율이 향상된다.
예 3) 베이즈 오류율의 상한이 다음과 같음을 증명하여라. $$P(error) \leq \int \frac {2}{\frac {1}{P(w_1 | \mathbf {x})} + \frac {1}{P(w_2 | \mathbf {x})}} p(\mathbf {x}) d\mathbf {x}.$$
※ 일반화된 평균(Generalized Mean) 자료

예 4) 아래의 확률 분포를 이용해서 베이즈 오류율의 상한이 다음과 같음을 증명하여라. $$p(x | w_1) = \frac {\pi^{-1}}{1 + (x - \mu)^2)}, p(x | w_2) = \frac{\pi^{-1}}{1 + (x + \mu)^2)}$$ $$P(error) \leq \frac {2 P(w_1) P(w_2)}{\sqrt{1 + 4 \mu^2 P(w_1) P(w_2)}}$$ (※ $\int \frac{1}{ax^2 + bx + c} dx = \frac{2 \pi}{\sqrt {4ac - b^2}}$ for $b^2 < 4ac$)

멀티 클래스 분류(Multi-Class Classification)
생선을 이제 농어군 $w_1$, 연어군 $w_2$, 잉어군$w_3$으로 세 가지 클래스로 분류해보자. 또 생선을 관찰하는 데 있어서 생선의 길이 $x_1$뿐만 아니라 너비 $x_2$와 밝기 $x_3$까지 고려해보자.
- $w_1, w_2, w_3$: 생선 클래스의 집합
- $\mathbf {x} \in \mathbb {R}^d$: 생선의 길이, 너비, 밝기를 포함하고 있는 특성 벡터(Feature Vector)
- 사전 확률 $P(w_1) + P(w_2) + P(w_3) = 1$
- 우도 $p(\mathbf {x} | w_j)$
1. Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification (2nd Edition). Wiley-Interscience, USA.
'Informatik' 카테고리의 다른 글
[Machine Learning] PCA(Principal Component Analysis) (0) 2022.02.09 [Machine Learning] 최대우도법 vs. 베이즈 추정법(Maximum Likelihood Estimation vs. Bayesian Estimation) (0) 2022.01.31 [Machine Learning] 단순 선형 회귀(Simple Linear Regression) (0) 2022.01.28 [Machine Learning] 회귀(Regression) (0) 2022.01.23 [Machine Learning] 선형 분류(Linear Classification) (0) 2022.01.20