[Machine Learning] 편향-분산 분해(Bias-Variance Decomposition)

편향-분산 분해는 지도 학습(Supervised Learning) 알고리즘의 오버 피팅(Overfitting)을 예방하기 위해 기대 오차(Expected Error)를 분석하는 방법이다. 오차를 편향, 분산 그리고 데이터 자체에 내재하고 있어 어떤 모델링으로 줄일 수 없는 오류의 합으로 본다. [wikipedia]

---

모수의 통계(Statistics of Parameter)

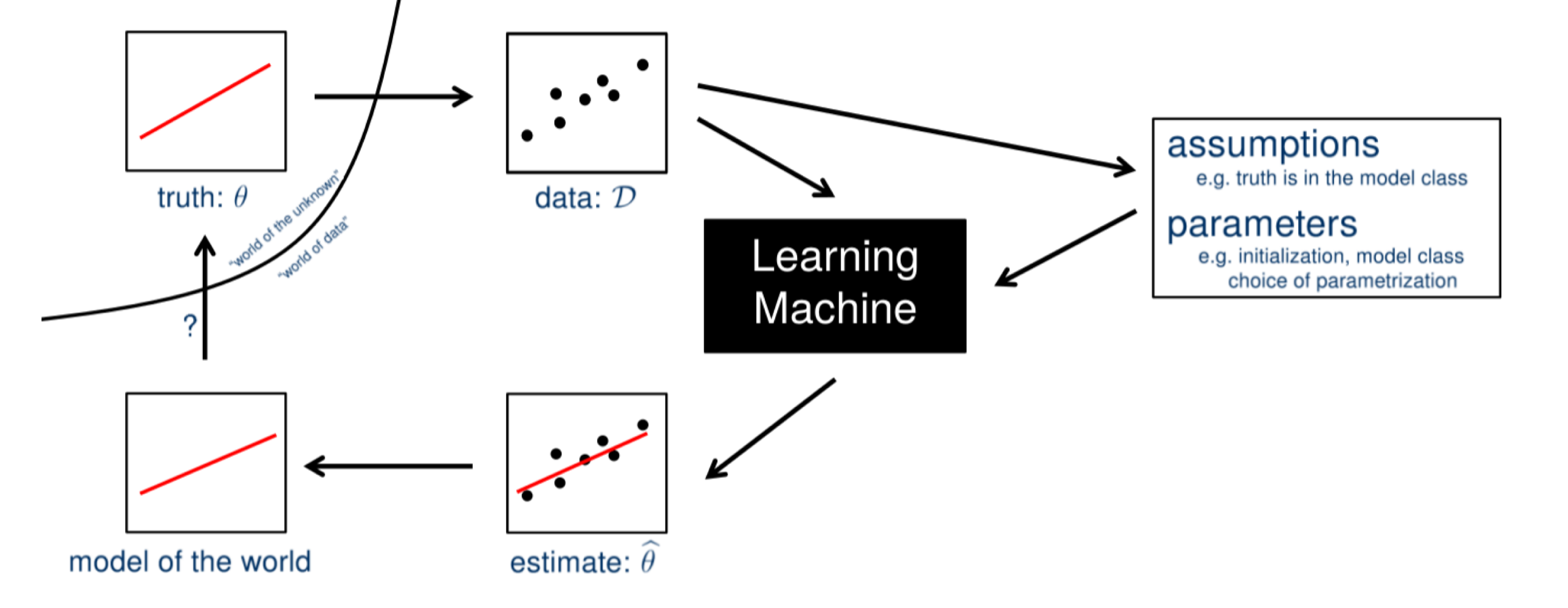
머신러닝은 미지수의 모수(Unknown Parameter) $\theta$에 생성되는 데이터 $\mathcal {D}$를 관찰 및 가정하여 모델을 학습하고 추정한 모수 $\hat {\theta}$에 대하여 관찰되지 않은 데이터들까지 가정에 들이 맞는지 모델을 평가하고 알맞은 모델을 선택한다. 좋은 머신러닝 모델이란, 미지수 모수 $\theta$와 그의 추정량 $\hat {\theta}$의 값의 차이가 작은, 즉, 가정과 사실이 일치하는 모델을 말한다.

$$Error(\hat {\theta}) = (\theta - \hat {\theta})^2$$

• 모수 $\theta$는 $\mathbb {R}^h$상의 값이다.
• $X_i$를 데이터의 확률 변수라고 할 때, 모수의 추정량 $\hat {\theta}$는 데이터 $\mathcal {D} = {X_1, \cdots, X_N}$의 함수이다.

모수의 추정량 $\hat {\theta}$을 다음과 같은 수치로 나타낼 수 있다. (※ $\theta \in \mathbb {R}^h$에 대해서 $\theta^2 = \theta^{\top} \theta$ 표기법을 사용한다.)

• 편향(Bias): 평균의 기대 편차. $$Bias(\hat {\theta}) = \mathbb {E} [\hat {\theta} - \theta]$$
• 분산(Variance): 평균 추정량의 산란도. $$Var(\hat {\theta}) = \mathbb {E} [(\hat {\theta} - \mathbb {E} [\hat {\theta}])^2]$$
• MSE: 일반화 오차(Generalized Error). $$MSE(\hat {\theta}) = \mathbb {E} [(\hat {\theta} - \theta)^2]$$

아래의 그림은 모수의 추정량 $\hat {\theta}$의 편향과 분산의 대소에 따라 달라지는 오차를 가시적으로 표현했다. 편향과 분산 모두 작을수록 모수의 참값에 가장 가깝게 추정을 할 수 있음을 확인할 수 있다.

---

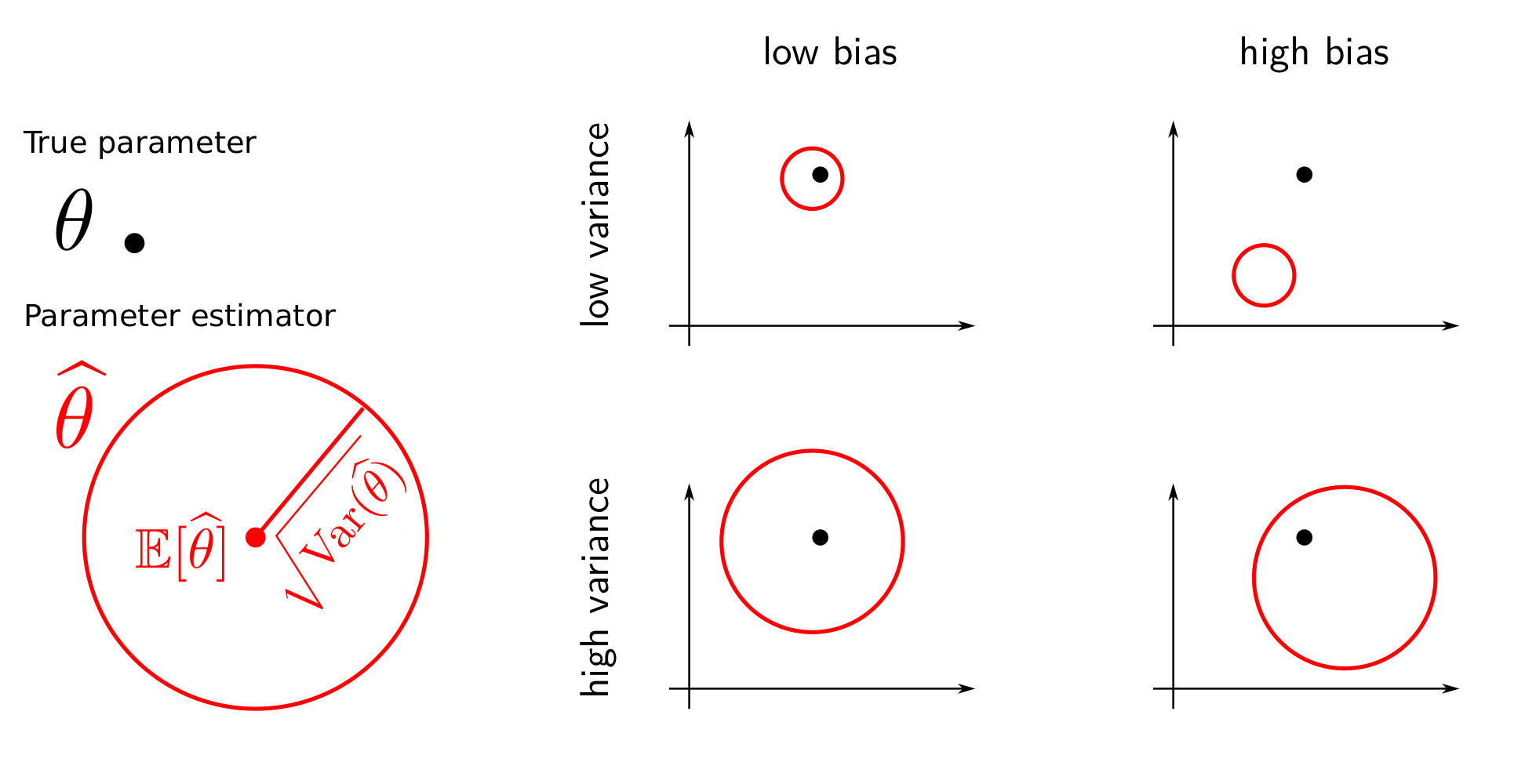
일반화 오차의 편향-분산 분해

예 1) $MSE(\hat {\theta}) = Bias (\hat {\theta})^2 + Var (\hat {\theta})$

일반화 오차가 편향과 분산으로 이루어져 있음을 증명하여라. (※ $\mathbb {E} [\hat {\theta}]= \hat {\theta}$)

---

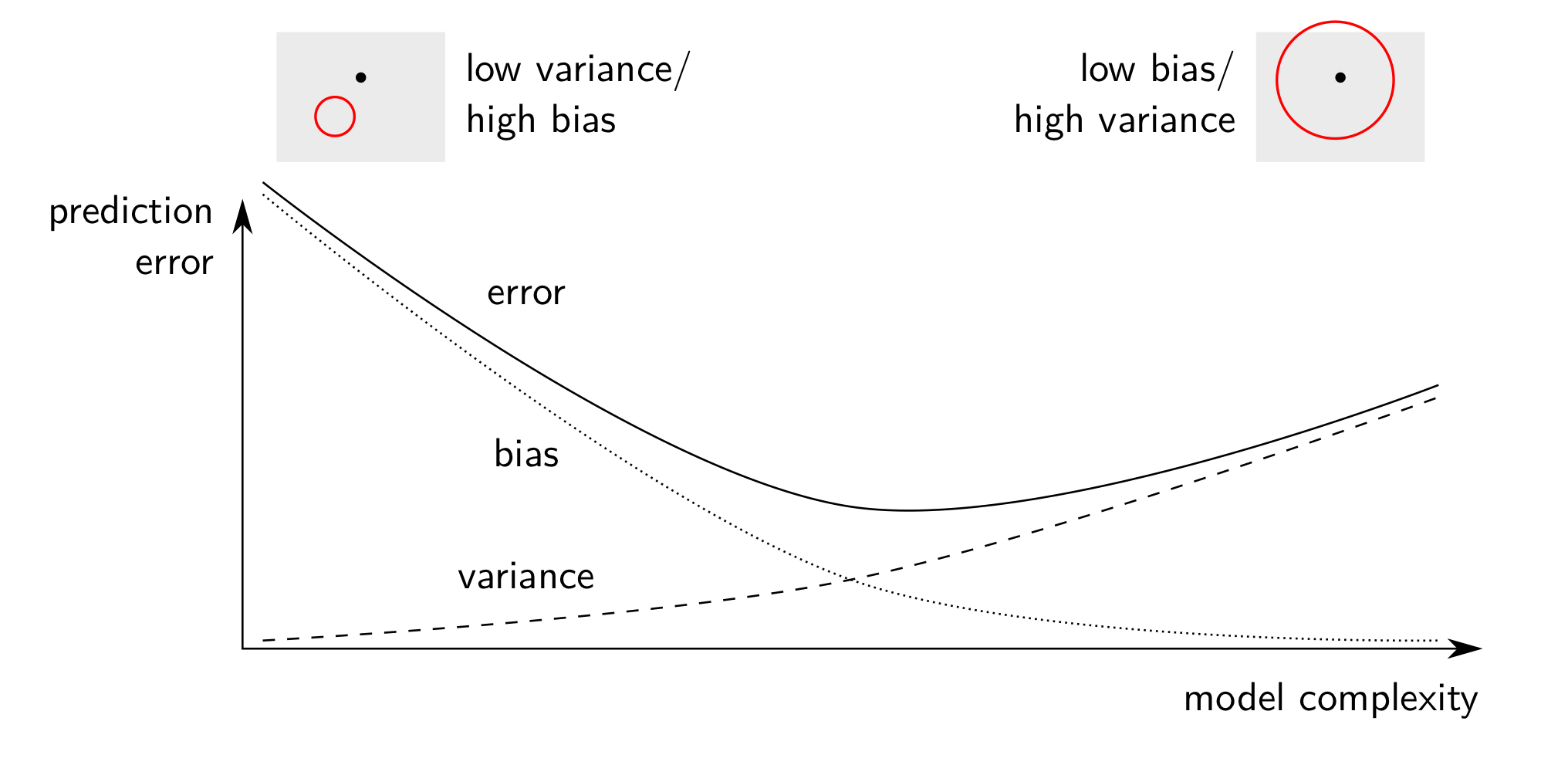
편향과 분산이 모두 작은 추정값을 찾으면 좋겠지만 실상은 모델의 복잡도가 증가하면서 오차를 구성하는 편향은 감소하고 분산은 증가하는 반비례 관계를 갖는다. 이때, 편향과 분산이 동시에 적절히 최저인 점을 스위트 스폿(Sweet Spot)이라고 하며 이 지점을 목표로 학습을 하도록 한다. 스위트 스폿 이전 모델의 단순함으로 오차가 큰 현상을 언더 피팅(Underfitting)이라고 하며, 스위트 스팟 이후 오차가 증가하는 현상을 오버 피팅이라고 한다.

---

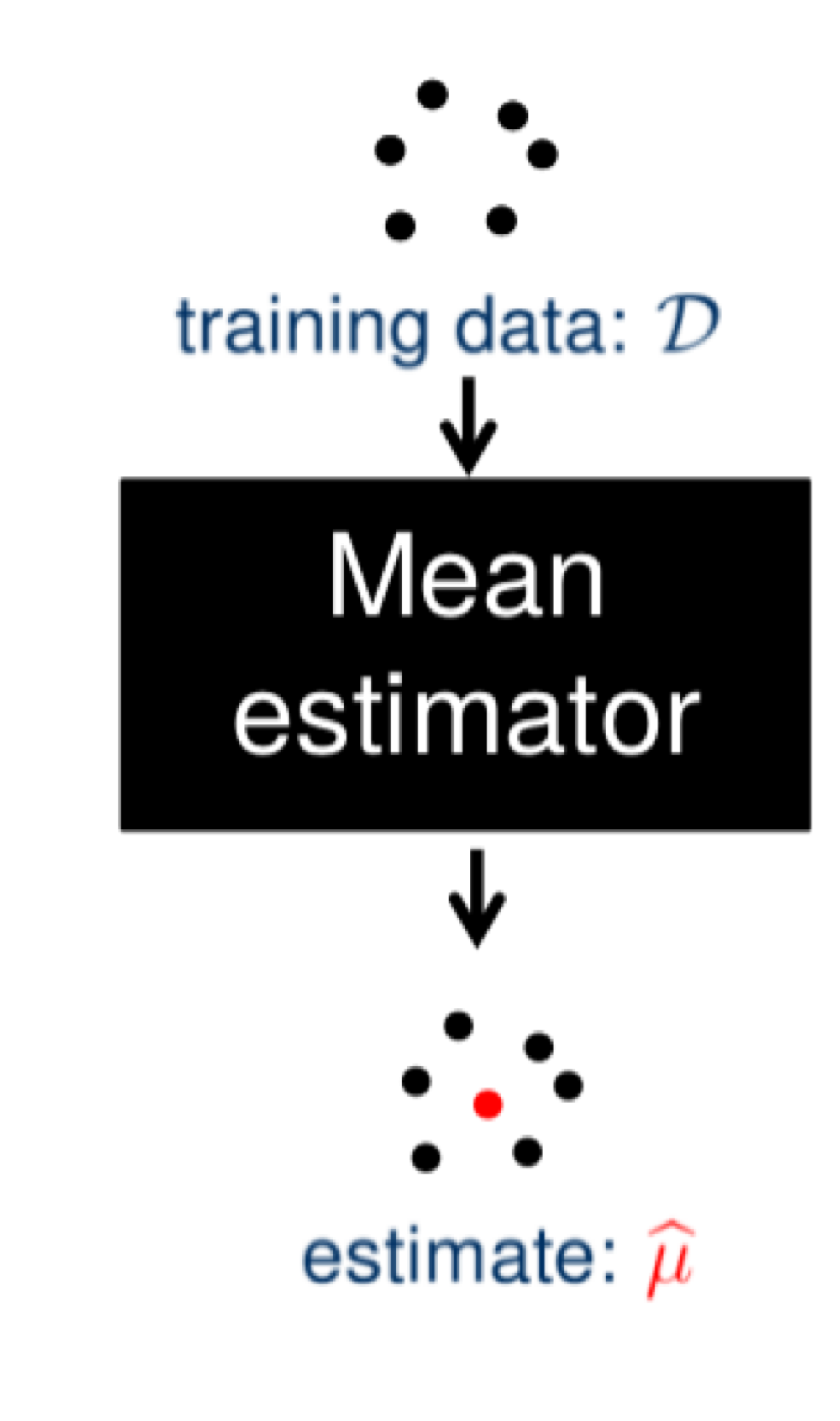
예 2) 가우시안 분포(Gaussian Distribution)의 모수

• 모수 $\theta$는 $\mathbb {C}^n$상의 값이다.
• $X_i$를 데이터의 확률 변수라고 할 때, 모수의 추정량 $\hat {\theta}$는 데이터 $\mathcal {D} = {X_1, \cdots, X_N}$의 함수이다.
• 평균 추정량(Mean Estimator): $\hat {\mu} = \frac {1}{N} \sum^{N}_{i = 1} X_i$
• 공분산 추정량(Covariance Estimator): $\hat {\Sigma} = \frac {1}{N - 1} (X_i - \hat {\mu})(X_i - \hat {\mu})^{\top}$

평균 추정량 $\hat {\mu}$가 $Bias(\hat {\mu}) = 0$와 $Var(\mu) = \frac {\sigma^2}{N}$임을 증명하여라.

편향이 $0$은 추정량의 기댓값이 모수와 같음을 의미며, 이러한 추정량를 불편 추정량(Unbiased Estimator)라고 한다. 이런 경우에서는 분산에 따라 일반화 오차의 크기가 갈린다. 또한, 가우시안 분포의 평균 추정량의 분산 $Var(\hat {\mu})$은 데이터의 개수 $N$에 반비례함을 증명했다. 즉, 데이터의 개수 $N$가 클수록 분산은 감소하며, 이에 따라 일반화 오차도 함께 감소한다.

---

※ [Machine Learning] 제임스-스타인 추정량(James-Stein Estimator)

[Machine Learning] 제임스-스타인 추정량(James-Stein Estimator)

---

예 3) 평균 $\mu$, 분산 $\sigma^2$를 갖는 확률 변수 $X_i$

모수 추정량 $\hat {\mu} = \alpha \frac {1}{N} \sum^N_{i = 1} X_i, \text{where } \alpha \text{ is a parameter between } [0,1]$의 편향, 분산, MSE를 구하여라.

---

예 4) 가우시안 노이즈(Gaussian Noise)가 있는 함수 $y = f(x) + \epsilon$의 편향-분산 분해

모델

$y = f(x) + \epsilon$, where

• 미지수 함수 $f: \mathbb {R}^n \rightarrow \mathbb {R}$.
• 독립적인 가우시안 노이즈 $\epsilon \sim \mathcal {N}(0, \sigma^2)$ 

  ---

가정

• 확률 분포(Probability Distribution) $P(x, y)$에서 독립적으로 생성된 학습 세트(Training Set) $\mathcal {D} = (x_1, y_1), \cdots, (x_m, y_m) \in \mathbb {R}^n \times \mathbb {R}$
• 가설 공간(Hypothesis Space) $\mathcal {H} = {h: \mathbb {R}^n \rightarrow \mathbb {R}}$
• $\mathcal {D}$에 기반한 가설 $h_{\mathcal {D}} \in \mathcal {H}$을 선택하는 학습 알고리즘 $L$

  ---

일반화 오차

• 가설 $h_{\mathcal {D}} \in \mathcal {H}$의 일반화 오차: $$Error [h_{\mathcal {D}}] = \mathbb {E}_{x, \epsilon} \left [ (h_{\mathcal {D}}(x) - y (x, \epsilon) )^2 \right ]$$
• 학습 알고리즘 $L$의 기대 일반화 오차: $$Error [L] = \mathbb {E}_{\mathcal {D}} \left [ \mathbb {E}_{x, \epsilon} \left [ (h_{\mathcal {D}}(x) - y (x, \epsilon) )^2 \right ] \right ]$$
• 학습 알고리즘 $L$의 기대 일반화 오차의 간단 표기법 $$Error [L] = \mathbb {E} \left [ (h_{\mathcal {D}}(x) - y (x, \epsilon) )^2 \right ] $$
• 학습 알고리즘 $L$의 기대 가설 $$h^*(x) = \mathbb {E}_{\mathcal {D}} [h_{\mathcal {D}}(x)]$$

  ---

학습 알고리즘 $L$의 기대 일반화 오차의 편향-분산 분해

$$ \mathbb {E} \left [ (h_{\mathcal {D}} - y)^2 \right ] = \underbrace { \mathbb {E} \left [ (f(x) - h^* (x))^2 \right ]}_{bias^2} + \underbrace {\mathbb {E} \left [ (h_{\mathcal {D}} (x) - h^* (x))^2 \right ]}_{variance} + \underbrace {\sigma^2}_{noise}$$

---

증명

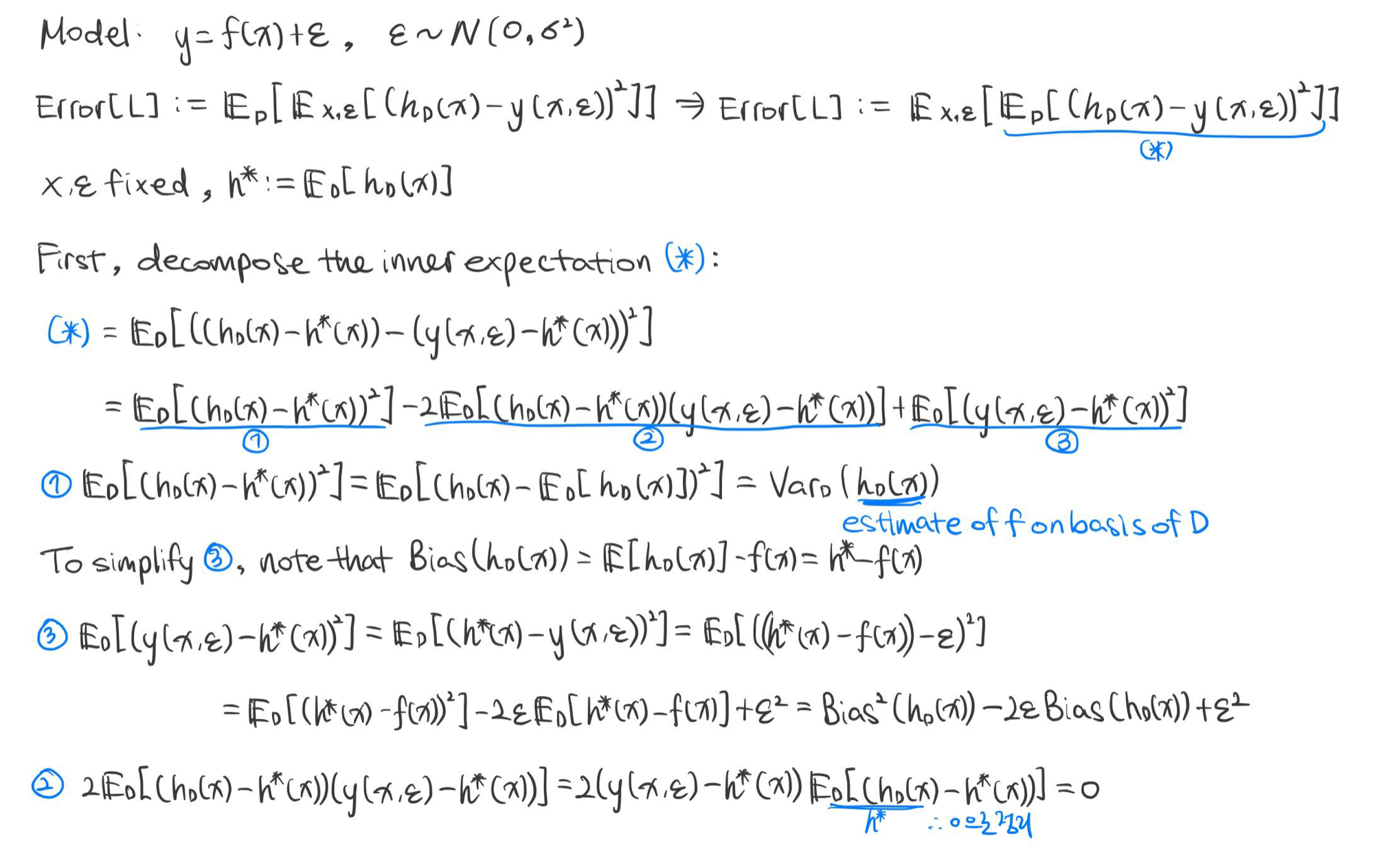
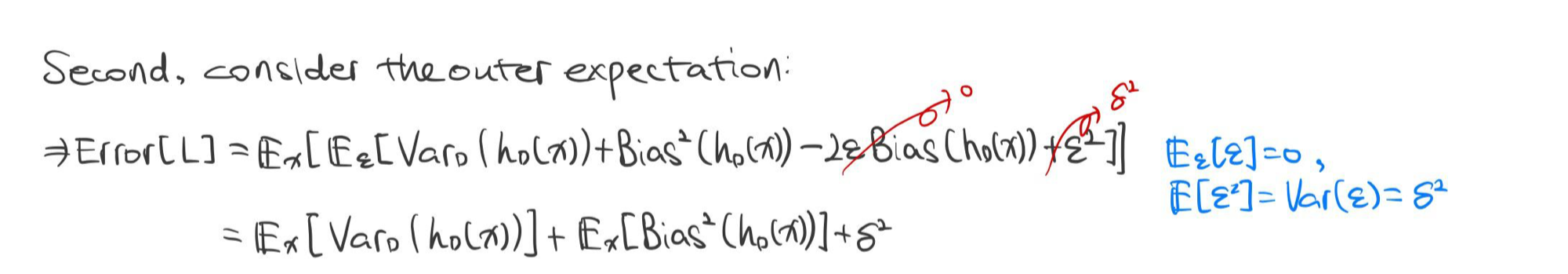
※ 참고

$$\begin {align*} \mathbb {E} [(y - \hat {f})^2] &=  \mathbb {E} [y^2 + \hat {f}^2 - 2y \hat {f}] \\ &=  \mathbb {E} [y^2] +  \mathbb {E} [\hat {f}^2] - \mathbb {E} [2y \hat {f}] \\ &= (Var [y] +  \mathbb {E} [y]^2) + (Var [\hat {f}] +  \mathbb {E} [\hat {f}]^2) - 2f  \mathbb {E} [\hat {f}] \\ &= Var [y] + Var [\hat {f}] + (f - \mathbb {E} [\hat {f}])^2 \\ &= Var [y] + Var [\hat {f}] + \mathbb {E}[f - \hat {f}]^2 \\ &= \sigma^2 + Var [\hat {f}] + Bias [\hat {f}]^2 \end {align*}$$

$$\begin {align*} Var [y] &= \mathbb {E} [(y - \mathbb {E} [y])^2] \\ &= \mathbb {E} [(y - f)^2] \\ &= \mathbb {E} [(f + \epsilon - f)^2] \\ &= \mathbb {E} [\epsilon^2] \\ &= Var [\epsilon] + \mathbb {E} [\epsilon]^2 \\ &= \sigma^2 \end {align*}$$

$$\mathbb {E} [y] = \mathbb {E} [f + \epsilon] = \mathbb {E}[f] = f$$

---

편향 및 분산 근사화(Bias and Variance Approximation)

$\begin {align*} \mathcal {D}_1, \cdots, \mathcal {D}_L &= \text {training sets of size } m \\ \mathcal {D}_{test} &= \text {test set of size } p \end {align*}$

• 학습 알고리즘 $L$의 기대 가설 $\mathbb {E}_{\mathcal {D}} [h_{\mathcal {D} (x)}]$: $$\hat {h}^* (x) = \frac {1}{L} \sum^L_{l = 1} h_{\mathcal {D}_l} (x)$$
• 학습 알고리즘 $L$의 기대 편향 제곱 $\mathbb {E} \left [ (f(x) - h^*(x))^2 \right ]$: $$\hat {\mathbb {E}}_{bias} = \frac {1}{p} \sum^p_{i = 1} \left ( f(x_i) - \hat {h}^* (x_i) \right )^2$$
• 학습 알고리즘 $L$의 기대 분산 $\mathbb {E} \left [ (h_{\mathcal {D}} (x) - h^*(x))^2 \right ]$: $$\hat {\mathbb {E}}_{var} = \frac {1}{p} \sum^p_{i = 1} \frac {1}{L} \sum^L_{l = 1} \left ( h_{\mathcal {D}_l} (x_i) - \hat {h}^* (x_i) \right )^2$$

---

학습 오차와 검정 오차 분석

아래의 통계는 다중 선형 회귀(Multiple Linear Regression)에서 다항식 기저 함수를 갖는 모델을 학습했을 때의 학습 오차, 검정 오차, 편향, 분산을 보여준다. $k$는 차수를 뜻하며, x 좌표는 학습 데이터 세트의 개수 $m$을 보여준다.

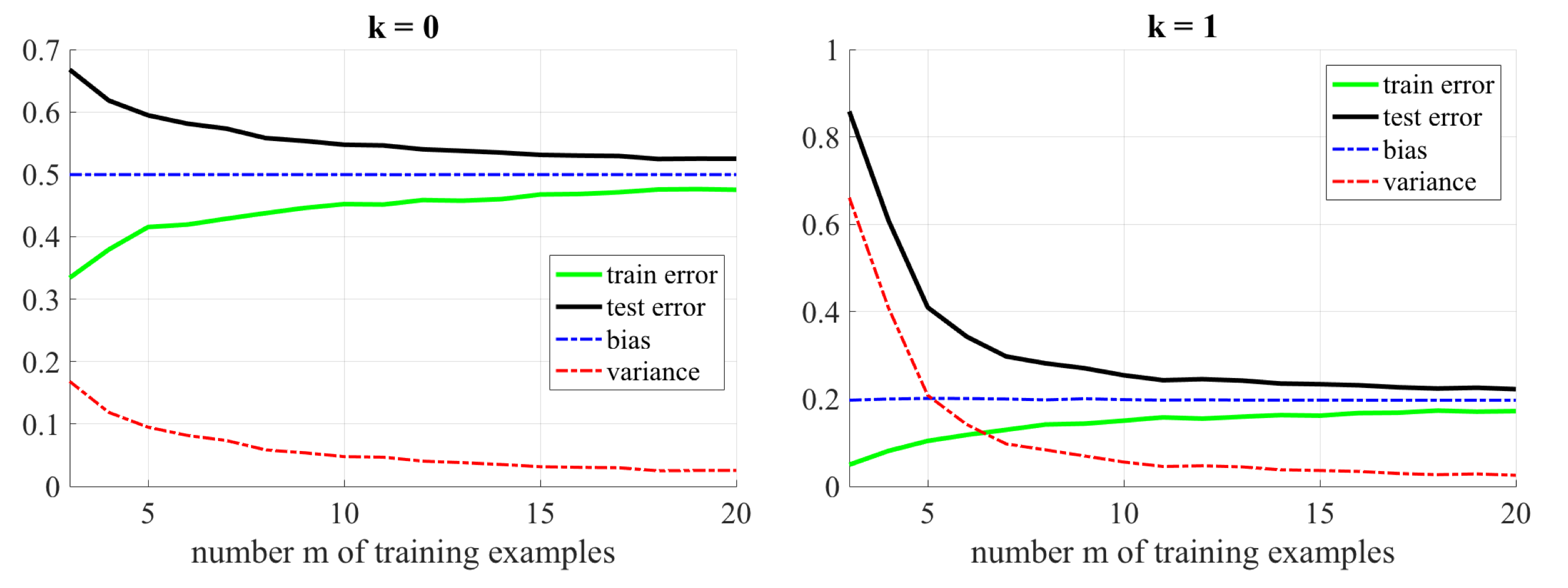
두 개의 모델을 살펴봤을 때, 학습 세트의 개수는 편향에 영향을 끼치지 않는다. 통계학적으로 데이터의 양이 많아질수록 분산은 작아지는 사실을 생각하면, 분산에 영향을 받는 검정 오차는 분산을 따라 함께 따라 감소하였다. 

아래의 통계는 각각 편향과 분산이 큰 값을 가질 때, 학습 오차와 검정 오차를 보여준다.

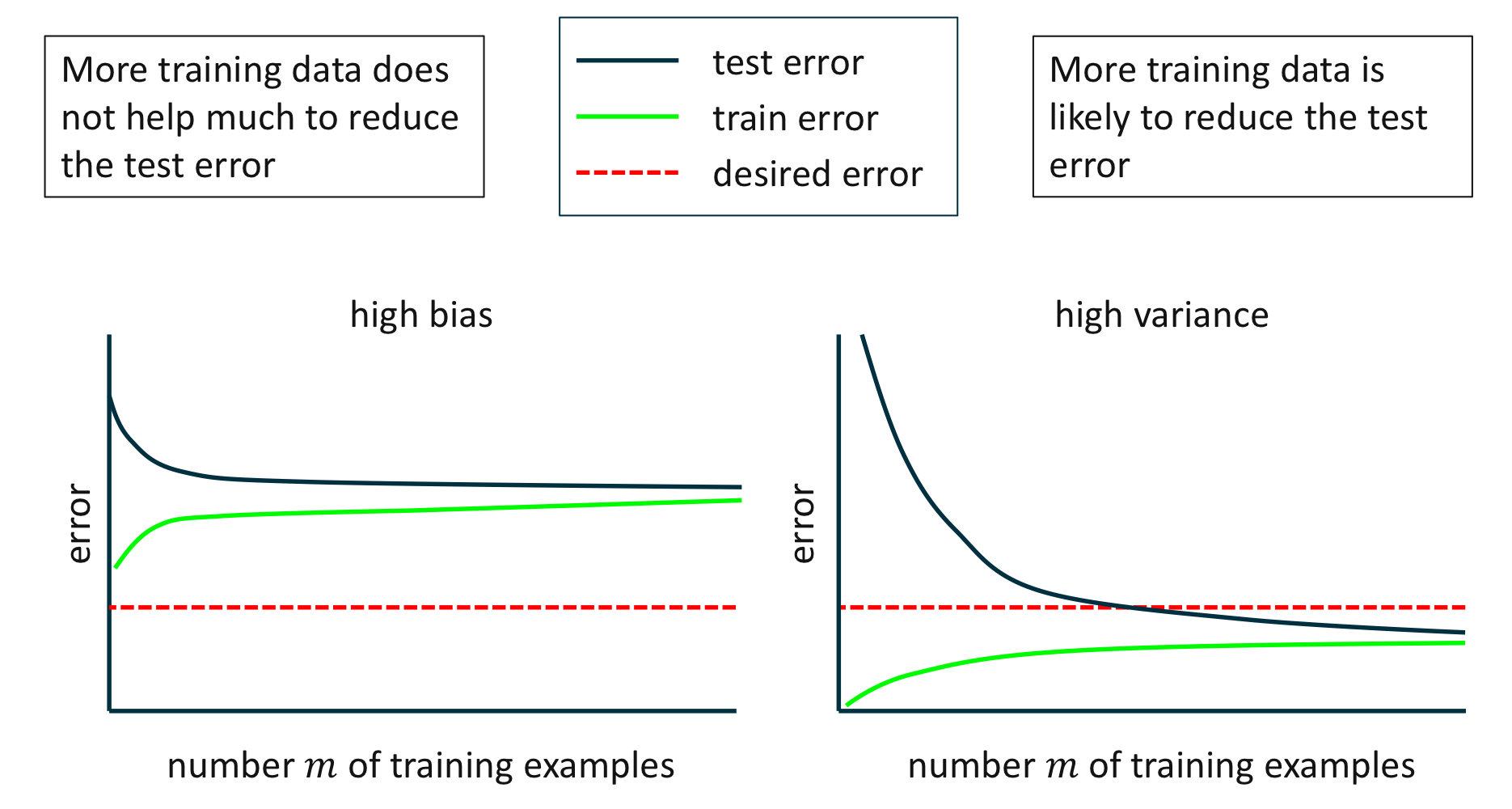
편향이 큰 값을 가질 경우, 학습 세트의 개수 $m$이 증가하더라도 검정 오차는 장기적으로 크게 영향을 받지 않는다. 이는 이전 통계에서 확인했듯이, 학습 세트의 개수가 편향에 크게 영향을 끼치지 않기 때문이다. 반면 분산이 큰 값을 가질 경우, 학습 세트의 개수가 증가하면서 검정 오차는 더 향상되었다.

따라서 다음과 같은 결론에 도달할 수 있다. 학습 모델을 관찰했을 때,

학습 오차가 크고, 검정 오차도 크다.	학습 오차가 작은데, 검정 오차가 크다.
- 편향이 작다. - 아직 학습이 미완성이다. - 더 유연한 모델을 사용할 필요가 있다. - 더 큰 가설 공간을 고려한다. - 더 많은 특성을 사용한다. - 정규화 모수(Regularization Parameter)를 감소시킨다.	- 분산이 크다. - 더 많은 학습 데이터 세트를 학습한다. - 특성을 감소시킨다. - 정규화 모수를 증가시킨다.

 

---

1. Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification (2nd Edition). Wiley-Interscience, USA.

2. Müller, K.R., Montavon, G. (2021). Lecture on Machine Learning 1-X. Technische Universität Berlin, Berlin, Germany.