[Machine Learning] 퍼셉트론 인공신경망(Perceptron Artificial Neural Network)

※ [Machine Learning] 선형 분류(Linear Classification)

[Machine Learning] 선형 분류(Linear Classification)

※ [Machine Learning] NCC(Nearest Centroid Classifier)

[Machine Learning] NCC(Nearest Centroid Classifier)

---

프랑크 로젠블라트(Frank Rosenblatt)가 패턴 인식(Pattern Recognition)을 위한 인공신경망(Artifical Neural Network)인 퍼셉트론(Perceptron)을 고안하였다. [Rosenblatt, 1958]

---

퍼셉트론 학습 알고리즘(Perceptron Learning Algorithm)

목표

다변량 데이터(Multivariate Data) $\mathbf {x} \in \mathbb {R}^{D}$를 이진 분류하여라.

입력

학습률(Learning Rate) $\eta$ and $N$ 튜플(Tuple) $(\mathbf {x}_n, y_m)$

• $D$ 차원의 데이터 $\mathbf {x}_n \in \mathbb {R}^{D}$
• 각 데이터에 대한 레이블 $y_n \in \{ -1, +1 \}$

출력

가중치 벡터(Weight Vector) $\mathbf {w} \in \mathbb {R}^{D}$

$$\mathbf {w}^{\top} \mathbf {x}_n - \beta =
\begin {cases}
\geq 0 & \text {if } y_n = +1 \\
< 0 & \text {if } y_n = -1
\end {cases}$$

※ 오프셋 및 편향(Offset or Bias)을 고려한 가중치는 $\tilde {\mathbf {w}} = (- \beta, \mathbf {w})$ $y$ 절편을 고려한 판별 함수를 간단하게 표현한다. 데이터 벡터도 마찬가지로 편향을 고려한 1을 덧 붙인 $\tilde {\mathbf {x}} = (1, \mathbf {x})$를 사용한다. 이렇게 하면 $\mathbf {w}^{\top} \mathbf {x} - \beta$ 대신 $\tilde {\mathbf {w}}^{\top} \tilde {\mathbf {x}}$를 사용한다.

$$\tilde {\mathbf {w}}^{\top} \tilde {\mathbf {x}} = 
\begin {cases}
\geq 0 & \text {if } y_n = +1 \\
< 0 & \text {if } y_n = -1
\end {cases}$$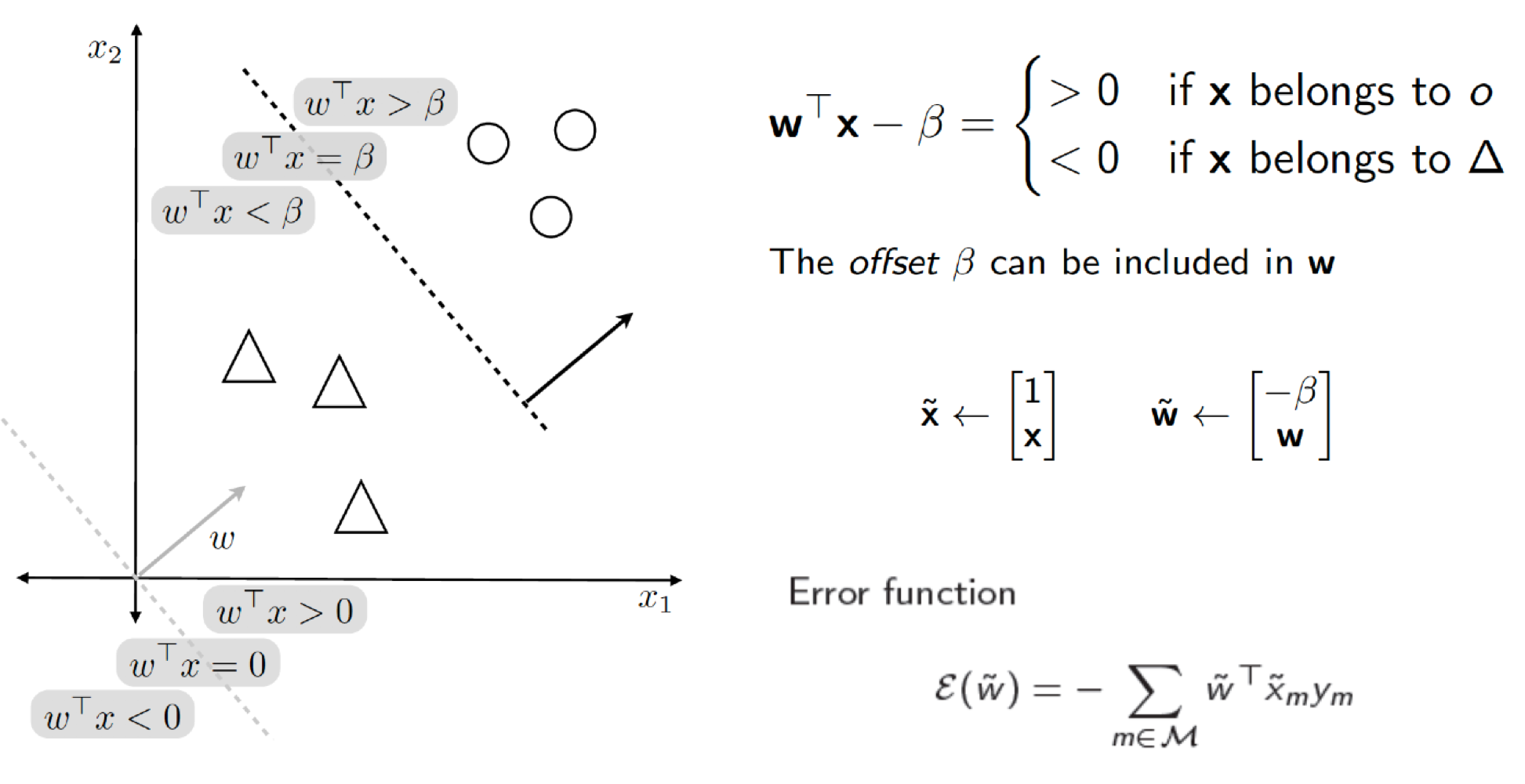

오차 함수(Error Function)는 올바르지 않게 분류되었을 때, 페널티를 부과하는 방식으로 다음과 같이 사용한다.

$$\mathcal {E} (\tilde {\mathbf {w}}) = - \sum_{m \in \mathcal {M}} \tilde {\mathbf {w}}^{\top} \tilde {\mathbf {x}}_m y_m$$

예를 들어, $\tilde {\mathbf {w}}^{\top} \tilde {\mathbf {x}}$의 결과가 $2$이고, $y_m$의 결과도 $1$일 때, 데이터가 클래스 $\circ$으로 올바르게 분류되었다. 두 결괏값의 곱은 $2 \times 1 = 2$이고 오차 함수에 의해 음수를 취하면 $-2$로 페널티가 부과되지 않는다. 반대로 $\tilde {\mathbf {w}}^{\top} \tilde {\mathbf {x}}$의 결과가 $2$이고, $y_m$의 결과는 $-1$일 때, 클래스 $\triangle$로 분류되었어야 할 데이터가 클래스 $\circ$로 잘못 분류되었다. 이때는 $-(2 \times -1) = 2$로 패널티가 부과된다. 즉, 데이터가 잘못 분류되었을 때 $\tilde {\mathbf {w}}^{\top} \tilde {\mathbf {x}} y_m$의 값은 음수이며, $\sum$ 앞에 있는 -에 의해 양수 값의 페널티가 부과된다.

퍼셉트론의 오차 함수는 확률적 경사 하강법(Stochastic Gradient Descent)으로 반복을 통해 최소화할 수 있다.

경사 하강법

1. 처음에 사용할 $\tilde {\mathbf {w}}^{old}$를 초기화한다. 예로, $\frac {1}{n}$으로 할당할 수 있다.
2. 모든 데이터가 정확히 레이블링될 때까지, 다음 절차를 반복한다.
   1. 임의의 잘못 분류된 데이터 $\tilde {\mathbf {x}}_m$를 선택한다.
   2. 데이터 $\tilde {\mathbf {x}}_m$에서 기울기 방향으로 하강한다.
      $$
      \begin {align*}
      \mathcal {E}_m (\tilde {\mathbf {w}}) &= - \tilde {\mathbf {w}}^{\top} \tilde {\mathbf {x}}_m y_m \\
      \nabla \mathcal {E}_m (\tilde {\mathbf {w}}) &= - \tilde {\mathbf {x}}_m y_m \\
      \tilde {\mathbf {w}}^{new} &\leftarrow \tilde {\mathbf {w}}^{old} - \eta \nabla \mathcal {E}_m (\tilde {\mathbf {w}}^{old}) \\
      \therefore \tilde {\mathbf {w}}^{new} &\leftarrow \tilde {\mathbf {w}}^{old} + \eta \tilde {\mathbf {x}}_m y_m
      \end {align*}
      $$

첫 번째 업데이트 후 임의로 선택했던 잘못 분류된 데이터 $\tilde {\mathbf {x}}_m$의 오차는 다음과 같다.

$$
\begin {align*}
- \tilde{\mathbf {w}}^{(new)\top} \tilde {\mathbf {x}}_m y_m &= - \tilde{\mathbf {w}}^{(old)\top} \tilde {\mathbf {x}}_m y_m - \eta (\tilde {\mathbf {x}}_m y_m)^{\top} \tilde {\mathbf {x}}_m y_m \\
&< - \tilde{\mathbf {w}}^{(old)\top} \tilde {\mathbf {x}}_m y_m
\end {align*}
$$

$$\because (\tilde {\mathbf {x}}_m y_m)^{\top} \tilde {\mathbf {x}}_m y_m > 0$$

Q. 어떤 경우에 퍼셉트론의 경사 하강법이 빨리 수렴되는가?
A. 두 클래스의 데이터들이 밀접하게 위치하고 있을 때, 더 정밀한 하이퍼플레인(Hyperplance)을 요구한다. 따라서 수렴하는데 더 많은 시간이 필요하다. 반대로, 두 클래스의 데이터들의 거리가 넓을 때, 더 빨리 수렴한다. 수학적으로 표현시, $||\tilde{\mathbf {w}}^{\top} \tilde {\mathbf {x}} - \beta|| > 0$일 때, 더 빨리 수렴한다.

---

퍼셉트론의 한계

항상 퍼셉트론으로 데이터를 이진 분류가 가능한 것은 아니다. 아래의 그림은 퍼셉트론의 경사 하강법이 수렴되지 않는 반례를 보여준다.

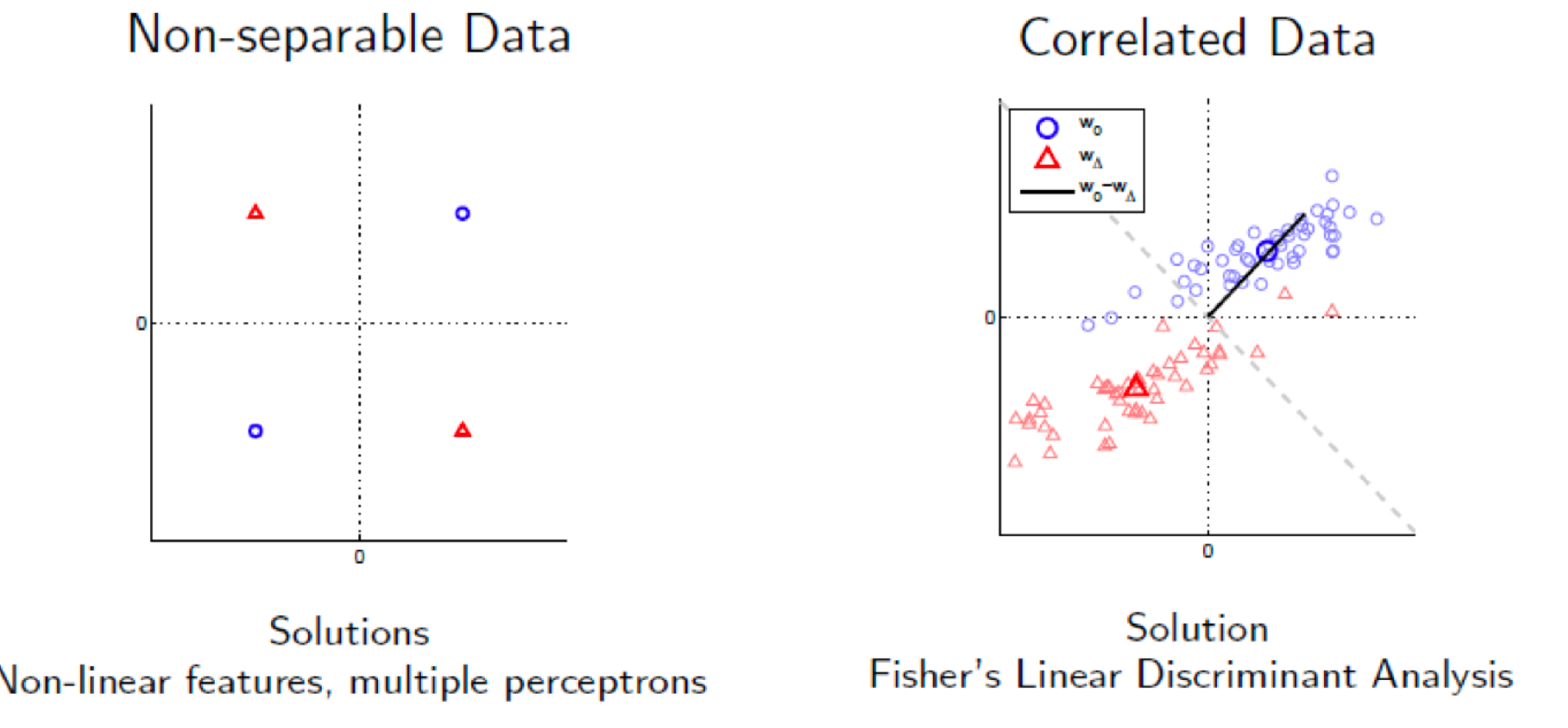
하나의 선형 모델로 분류될 수 없는 경우, 혹은 데이터가 서로 연관되어 있을 때, 퍼셉트론을 적용할 수 없다. 전자의 경우, 비선형 모델(Non-linear Model)을 사용하거나, 다중 퍼셉트론 모델(Multiple Perceptrons)으로 해결하고, 후자의 경우, 피셔의 선형 판별 분석(Fisher's Linear Discriminant Analysis)을 사용한다.

---

1. Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification (2nd Edition). Wiley-Interscience, USA.

2. Müller, K.R., Montavon, G. (2021). Lecture on Machine Learning 1-X. Technische Universität Berlin, Berlin, Germany.