-
[Machine Learning] NCC(Nearest Centroid Classifier)Informatik 2022. 2. 16. 17:55
※ [Machine Learning] 선형 분류(Linear Classifier)
[Machine Learning] 선형 분류(Linear Classifier)
선형 분류는 일차원 혹은 다차원 데이터들을 선형 모델(Linear Model)을 이용하여 클래스들로 분류(Classification)하는 머신러닝(Machine Learning) 기법이다. 아래 예시는 2차원 데이터를 어떤 선형 모델로
minicokr.com
머신러닝에서 NCC는 분류하고자 하는 데이터에서 가장 가까이 위치하고 있는 레이블링 된 데이터의 집합의 중심을 기준으로 분류하는 모델 중 하나다. [wikipedia]
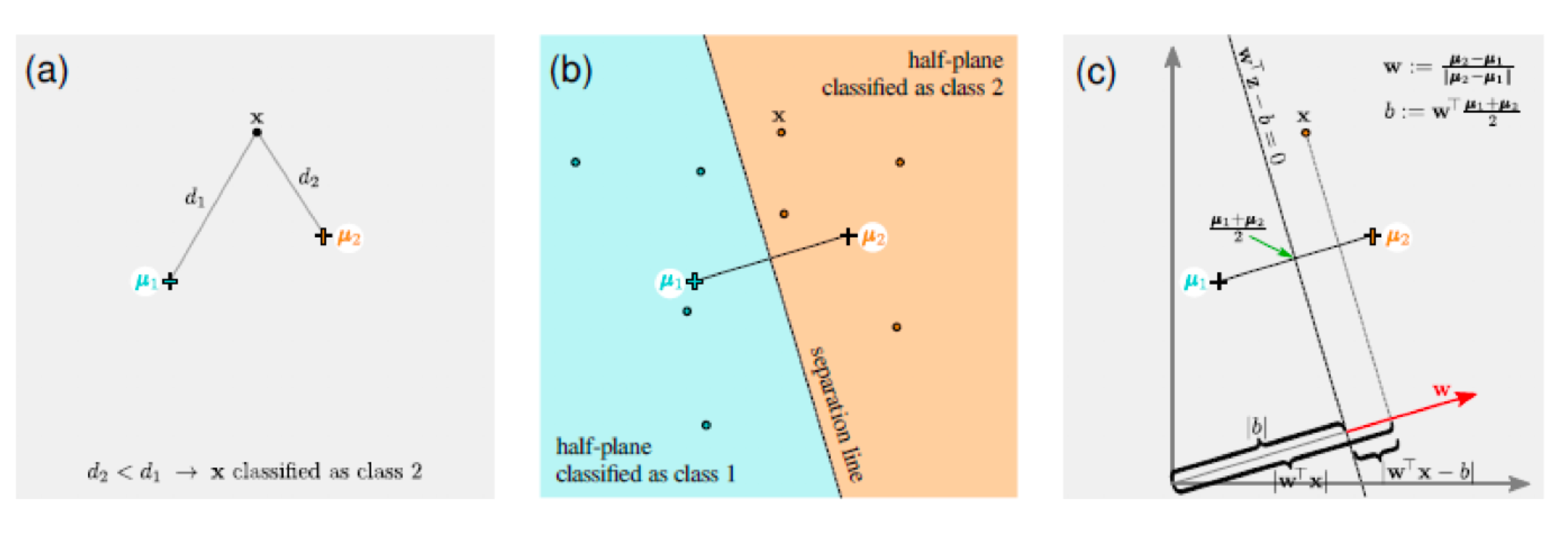
두 개의 중심 $\mu_1, \mu_2$과 각 레이블에 속하는 데이터들이 주어졌다고 가정하자. 새로운 데이터에서 두 개의 중심과의 최단 거리를 계산하고, 이 중 더 작은 거리를 갖는 레이블로 분류한다.
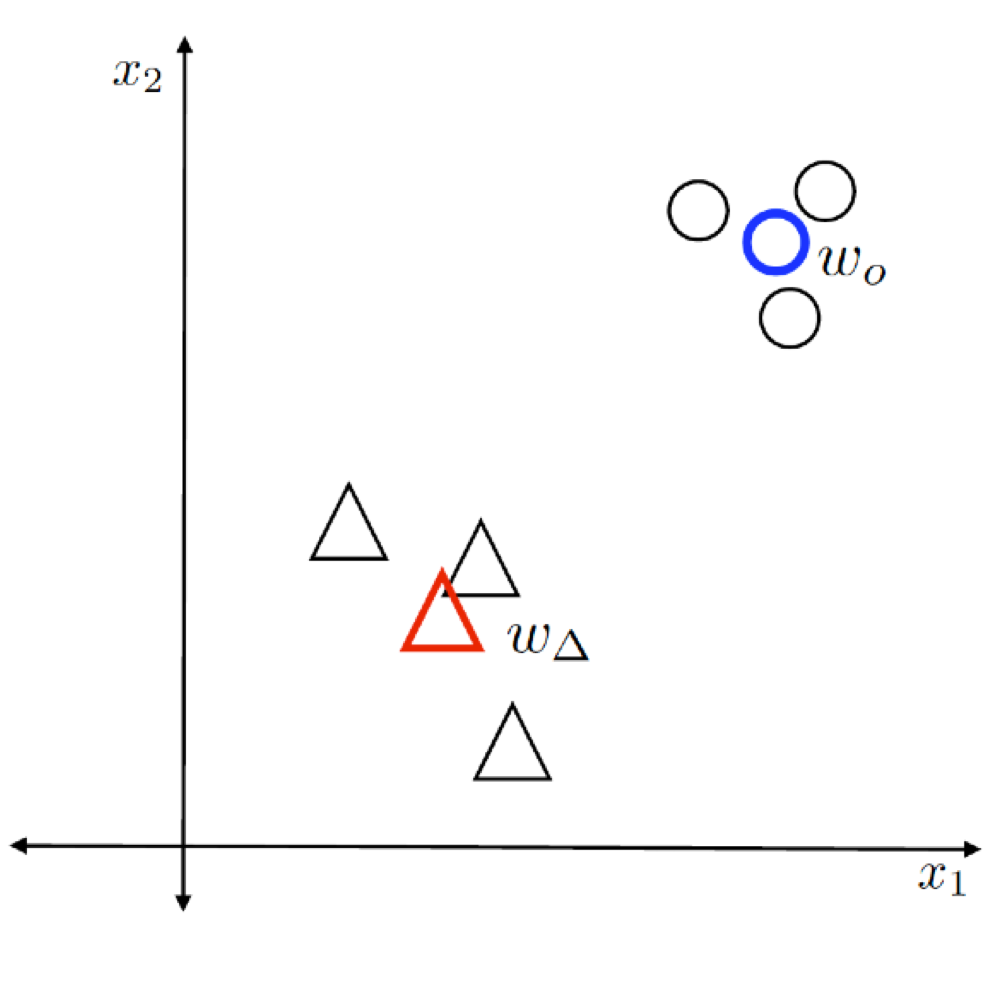
예 1)
두 개의 특성(Feature) $x_1, x_2$를 갖는 데이터 $\mathbf {x} \in \mathbb {R}^2$를 두 개의 클래스 $\mathbf {w}_{\triangle}, \mathbf {w}_{\circ}$로 분류하고자 한다.
NCC의 원리를 따라 각 클래스의 중심을 구한다.
$$\mathbf {w}_{\triangle} = \frac {1}{N_{\triangle}} \sum^{N_{\triangle}}_{n = 1} \mathbf {x}_{\triangle, n}$$
$$\mathbf {w}_{\circ} = \frac {1}{N_{\circ}} \sum^{N_\circ}_{n = 1} \mathbf {x}_{\circ, n}$$
새로운 데이터 $\mathbf {x}$에서 $\mathbf {w}_{\triangle}, \mathbf {w}_{\circ}$로의 각 최단 거리는 다음과 같다.
$$||\mathbf {w}_{\triangle} - \mathbf {x}|| = \sqrt {\sum^2_{j = 1} (\mathbf {w}_{\triangle j} - x_j)^2}$$
$$||\mathbf {w}_{\circ} - \mathbf {x}|| = \sqrt {\sum^2_{j = 1} (\mathbf {w}_{\circ j} - x_j)^2}$$
$||\mathbf {w}_{\triangle} - \mathbf {x}||$와 $||\mathbf {w}_{\circ} - \mathbf {x}||$의 대소를 비교하여 새로운 데이터 $\mathbf {x}$를 분류한다.
$$||\mathbf {w}_{\triangle} - \mathbf {x}|| > ||\mathbf {w}_{\circ} - \mathbf {x}||? \mathbf {x} \text { belongs to } \circ : \mathbf {x} \text { belongs to } \triangle$$
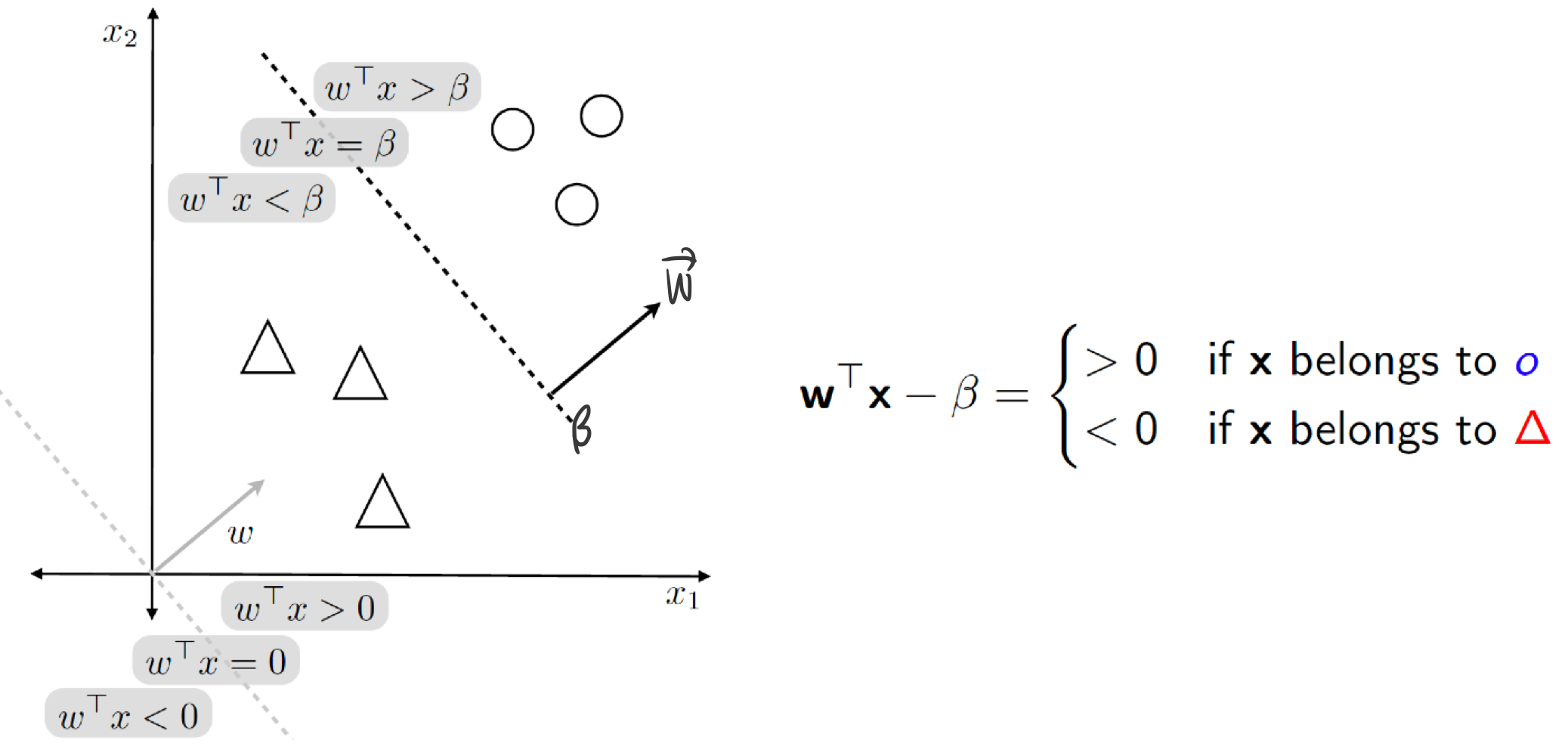
예를 들어, $distance (\mathbf {x}, \mathbf {w}_{\triangle}) > distance (\mathbf {x}, \mathbf {w}_{\circ})$를 정리하면,
$$\begin {align*} ||\mathbf {x} - \mathbf {w}_{\triangle}|| &> ||\mathbf {x} - \mathbf {w}_{\circ}|| \\ \Leftrightarrow ||\mathbf {x} - \mathbf {w}_{\triangle}||^2 &> ||\mathbf {x} - \mathbf {w}_{\circ}||^2 \\ \Leftrightarrow (\mathbf {x} - \mathbf {w}_{\triangle})^{\top} (\mathbf {x} - \mathbf {w}_{\triangle}) &> (\mathbf {x} - \mathbf {w}_{\circ})^{\top} (\mathbf {x} - \mathbf {w}_{\circ}) \\ \Leftrightarrow \mathbf {x}^{\top} \mathbf {x} - \mathbf {x}^{\top} \mathbf {w}_{\triangle} - \mathbf {w}^{\top}_{\triangle} \mathbf {x} + \mathbf {w}^{\top}_{\triangle} \mathbf {w}_{\triangle} &> \mathbf {x}^{\top} \mathbf {x} - \mathbf {x}^{\top} \mathbf {w}_{\circ} - \mathbf {w}^{\top}_{\circ} \mathbf {x} + \mathbf {w}^{\top}_{\circ} \mathbf {w}_{\circ} \\ \Leftrightarrow -2 \mathbf {w}^{\top}_{\triangle} \mathbf {x} + \mathbf {w}^{\top}_{\triangle} \mathbf {w}_{\triangle} &> -2 \mathbf {w}^{\top}_{\circ} \mathbf {x} + \mathbf {w}^{\top}_{\circ} \mathbf {w}_{\circ} \end {align*}$$
$$\begin {align*} \therefore distance (\mathbf {x}, \mathbf {w}_{\triangle}) &> distance (\mathbf {x}, \mathbf {w}_{\circ}) \\ ||\mathbf {x} - \mathbf {w}_{\triangle}|| &> ||\mathbf {x} - \mathbf {w}_{\circ}|| \\ \Leftrightarrow 0 &< {\underbrace {(\mathbf {w}_{\circ} - \mathbf {w}_{\triangle})}_{\mathbf {w}}}^{\top} \mathbf {x} - \underbrace {\frac{1}{2} (\mathbf {w}^{\top}_{\circ} \mathbf {w}_{\circ} - \mathbf {w}^{\top}_{\triangle} \mathbf {w}_{\triangle})}_{\beta} \end {align*}$$
이와 같은 판별 함수는 곧 선형 분류(Linear Classification)를 의미한다.
[Machine Learning] 퍼셉트론 인공신경망(Perceptron Artificial Neural Network)
[Machine Learning] 퍼셉트론 인공신경망(Perceptron Artificial Neural Network)
※ [Machine Learning] 선형 분류(Linear Classification) [Machine Learning] 선형 분류(Linear Classification) 선형 분류는 일차원 혹은 다차원 데이터들을 선형 모델(Linear Model)을 이용하여 클래스들로 분..
minicokr.com
1. Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification (2nd Edition). Wiley-Interscience, USA.
2. Müller, K.R., Montavon, G. (2021). Lecture on Machine Learning 1-X. Technische Universität Berlin, Berlin, Germany.
'Informatik' 카테고리의 다른 글
[Machine Learning] 상관계수(Correlation Coefficient) (0) 2022.02.16 [Machine Learning] 퍼셉트론 인공신경망(Perceptron Artificial Neural Network) (0) 2022.02.16 [Machine Learning] 편향-분산 분해(Bias-Variance Decomposition) (0) 2022.02.15 [Machine Learning] 제임스-스타인 추정량(James-Stein Estimator) (0) 2022.02.15 [Machine Learning] 모델 평가와 선택(Model Assessment and Selection) (0) 2022.02.14