[Machine Learning] 단순 선형 회귀(Simple Linear Regression)

※ [Machine Learning] 회귀(Regression)

[Machine Learning] 회귀(Regression)

통계학에서 선형 회귀는 종속 변수 $y$와 한 개 이상의 독립 변수 $X$와의 선형 상관관계를
모델링하는 회귀분석 기법이다. [wikipedia]

---

선형 회귀의 가정과 목표

※ 참고

$m$	학습 세트의 개수(Number of training examples)
$n$	특성의 개수(Number of features)
$\mathbf{x}_i = (x_{i1}, ..., x_{in})$	i 번째 학습 예시의 특성 벡터(Feature Vector of i-th training example)
$\mathbf {x}_{ij}$	i 번째 학습 예시의 j 번째 특성(j-th feature of i-th training example)
$y_i$	i 번째 학습 예시의 결과값(Ouput of i-th training example)

---

가정

다음과 같은 조건을 만족하는 학습 데이터 세트 $(\mathbf{x}_1, y_1), (\mathbf {x}_2, y_2),..., (\mathbf {x}_m, y_m)$를 가정하자.

$$y_i = f(\mathbf {x}_i) + \epsilon, \text { where } f: \mathbb {R}^n \rightarrow \mathbb {R} \text { is an unknown function and } \epsilon \sim \mathcal {N} (0, \sigma^2) \text { is a random error term.}$$

---

목표

알려지지 않은 함수 $f: \mathbb {R}^n \rightarrow \mathbb {R}$를 최대한 잘 예측하여라.

목표를 달성하기 위해서는 예측한 함수를 평가를 하는 도구가 필요하다. 따라서 ERM을 이용해 가정했던 함수 $f$가 최적한 지 평가한다.

---

기대 위험도(Expected Risk)

입력 출력 집합(Input-Ouput Space) $\mathcal {Z} = \mathbb {R}^n \times \mathbb {R}$에 대한 확률 분포(Probability Distribution) $P(\mathbf{x}, y)$, 손실 함수(Loss Function) $l(h(\mathbf{x}), y)$, 가설 공간(Hypothesis Space) $\mathcal {H} = {h: \mathbb {R}^n \rightarrow \mathbb {R}}$를 가정할 때, 가설 $h \in \mathcal {H}$에 대한 기대 위험도는 다음과 같다.

$$E[h] = \int_{\mathcal {Z}} l(h(\mathbf {x}), y) dP(\mathbf {x}, y)$$.

따라서 목표(알려지지 않은 함수 $f: \mathbb {R}^n \rightarrow \mathbb {R}$를 최대한 잘 예측하여라.)는 다음과 같이 해석된다.

---

목표

기대 위험도 $E [h]$를 최소화할 수 있는 가설 $h \in \mathcal {H}$을 찾아라.

여기서 문제는, 일반적으로 확률 분포 $P(\mathbf {x}, y)$가 알려지지 않았기 때문에 기대 위험도 $E [h]$를 계산할 수 없다. 따라서 기대 위험도 대신 경험적 위험도(Empirical Risk) $E_m [h]$를 최소화하는 ERM을 사용한다.

---

ERM(Empirical Risk Minimization)

제곱 손실 함수(Squared Loss Function):
$$l(h(\mathbf {x}), y) = \frac {1}{2} (h(\mathbf {x}) - y)^2$$
MSE(Mean Squared Error):
$$MSE = \frac {1}{2m} \sum^m_{i = 1} (h(\mathbf {x}) - y)^2$$

---

예 1) SLR의 ERM 최적화

• 선형 함수의 가설 공간: $x$에 대한 일차방정식으로 $w_0$가 $y$ 절편, $w_1$는 기울기에 해당한다. $$\mathcal {H} = \{ h_w(x) = w_0 + w_1 x | w = (w_0, w_1) \in \mathbb {R}^2 \}$$
• 가설: $$h_w(x) = w_0 + w_1 x$$
• 모수: $$w = (w_0, w_1), \text { where } w_0 \text { is bias and } w_1 \text { is weight}$$
• MSE: $$E_m [h_w] = \frac {1}{2m} \sum^m_{i = 1} (h_w(x_i) - y_i)^2 = \frac {1}{2m} \sum^m_{i = 1} (w_0 + w_1 x_i - y_i)^2$$
• 최적 모수:

---

이처럼 MSE에서 분석적으로 최적 모수를 구할 수 있지만 일반적으로는 불가능하다. 따라서 경사 하강법으로 최적 값을 대신 구할 수 있다. 

예 2) SLR의 ERM과 경사 하강법

가정

학습 데이터 세트(Training Dataset)$(\mathbf {x}_1, y_1), (\mathbf {x}_2, y_2), ..., (\mathbf {x}_m, y_m) \in \mathbb {R}^{n + 1} \times \mathbb {R}$를 가정하자.

---

목표

ERM 기법으로 다음 MSE를 최소화하여라.

$$J(\mathbf {w}) = \frac {1}{2m} \sum^{m}_{i = 1} (h_{\mathbf {w}}(\mathbf {x}_i) - y_i)^2 = \frac {1}{2m} (\mathbf {X} \mathbf {w} - \mathbf {Y})^{\top} (\mathbf {X} \mathbf {w} - \mathbf {Y})$$

※ 참고

$\mathbf {X}$	1이 결합된 데이터 행렬(Augmented Data Matrix)
$\mathbf {Y}$	출력 벡터(Output Vector)
$\mathbf {w}$	모수 벡터(Parameter Vector)

---

미분으로 최적의 $\mathbf {w}$ 구하기

$$\mathbf {w} = (\mathbf {X}^{\top} \mathbf {X})^{-1} \mathbf {X}^{\top} \mathbf {Y} \ \ \ \text {if } \mathbf {X}^{\top} \mathbf {X} \text { is non-singular}$$

증명)

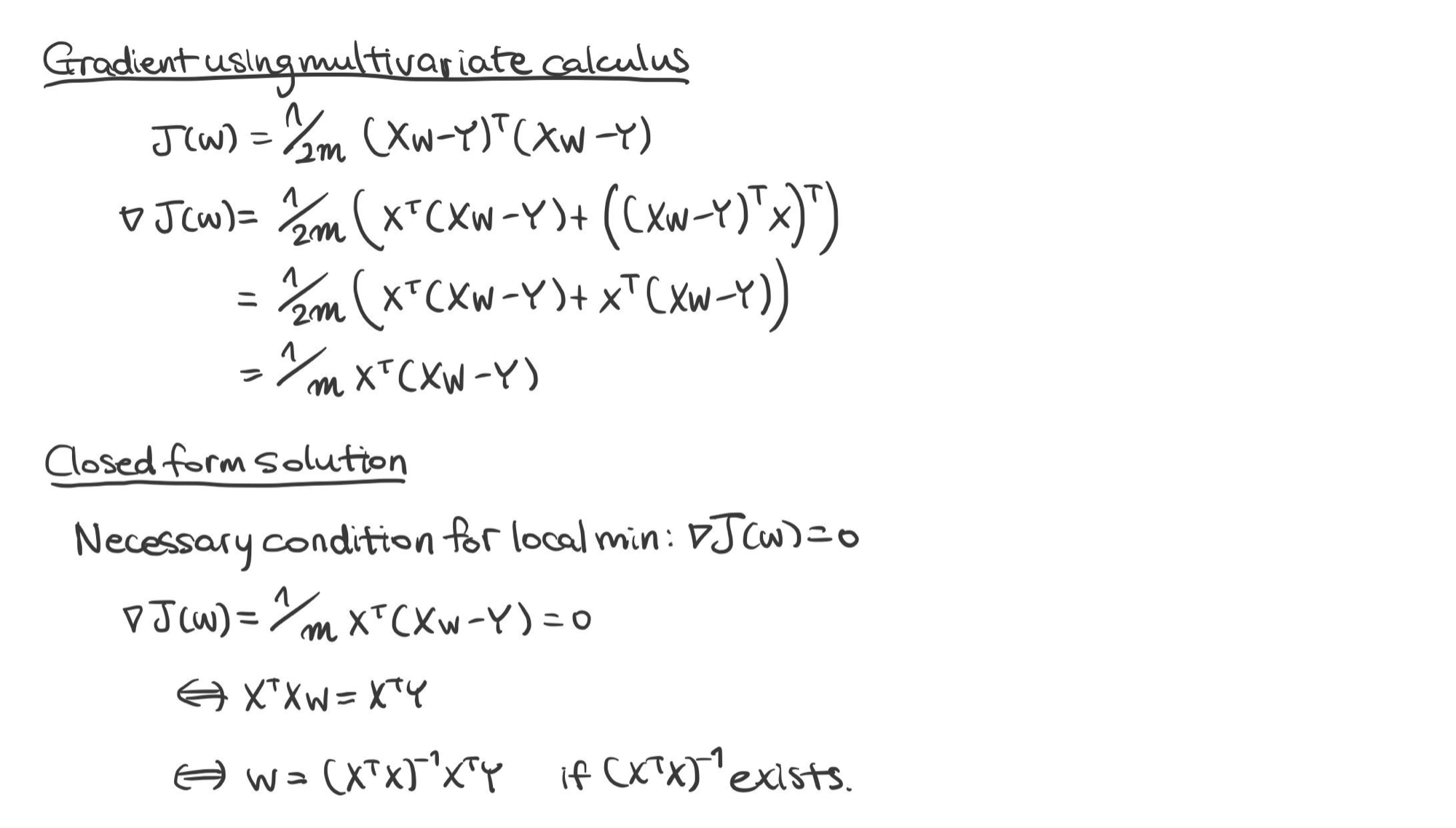
※ $\mathbf {X} \in \mathbb {R}^{n + 1, m}$일 때는 $\mathbf {w} = (\mathbf {XX}^{\top})^{-1} \mathbf {X} \mathbf {Y}$. 단, $(\mathbf {XX}^{\top})^{-1}$이 존재해야 한다.

검증)

---

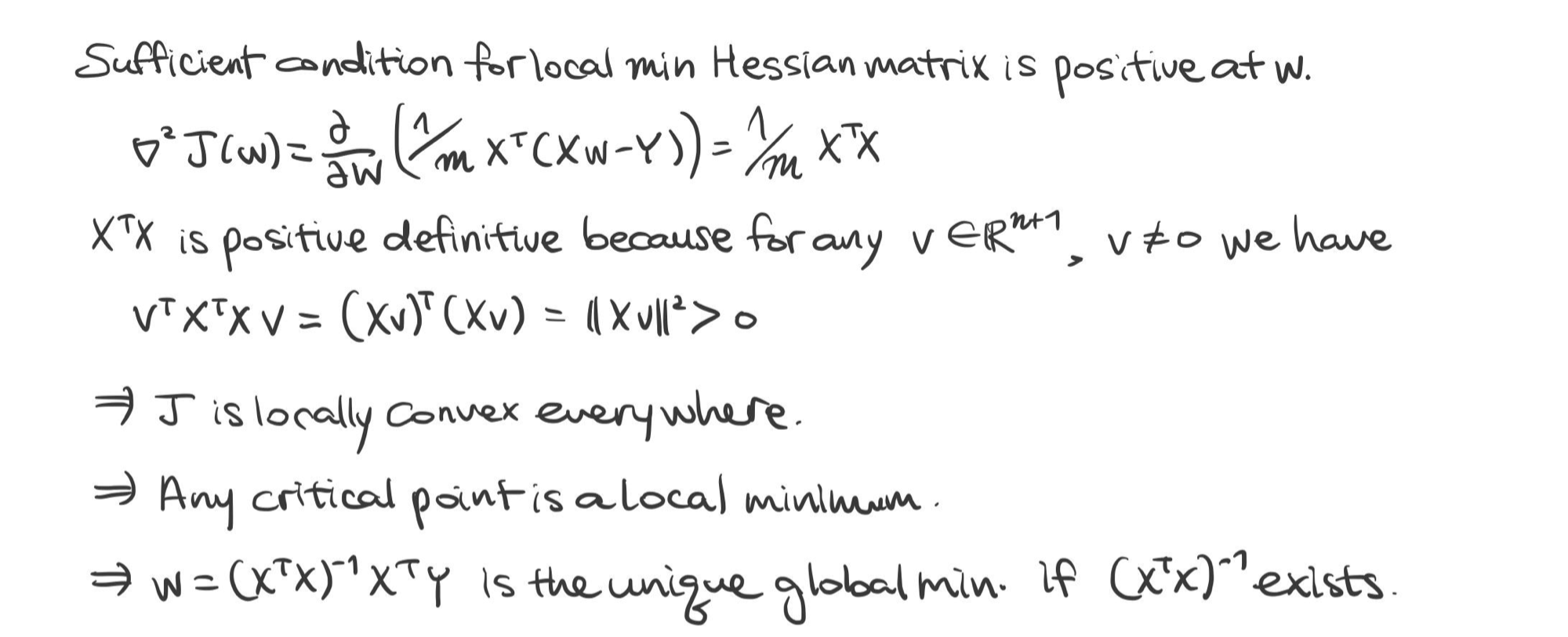
경사 하강법 적용

[Machine Learning] 경사 하강법(Gradient Descent)

$$w_j \rightarrow w_j - \eta \frac {\partial}{\partial w_j} J(\mathbf {w}) \ \ \ \text {for all } j$$ $$\therefore \mathbf {w} \rightarrow \mathbf {w} - \frac {\eta}{m} \mathbf {X}^{\top} (\mathbf {X} \mathbf {w} - \mathbf {Y})$$

---

※ [Machine Learning] 다중 선형 회귀(Multiple Linear Regression)

[Machine Learning] 다중 선형 회귀(Multiple Linear Regression)