[Machine Learning] 선형 분류(Linear Classification)

선형 분류는 일차원 혹은 다차원 데이터들을 선형 모델(Linear Model)을 이용하여 클래스들로 분류(Classification)하는 머신러닝(Machine Learning) 기법이다. 아래 예시는 2차원 데이터를 어떤 선형 모델로 $R_0$ 혹은 $R_1$로 분류하는 선형 분류를 보여준다.

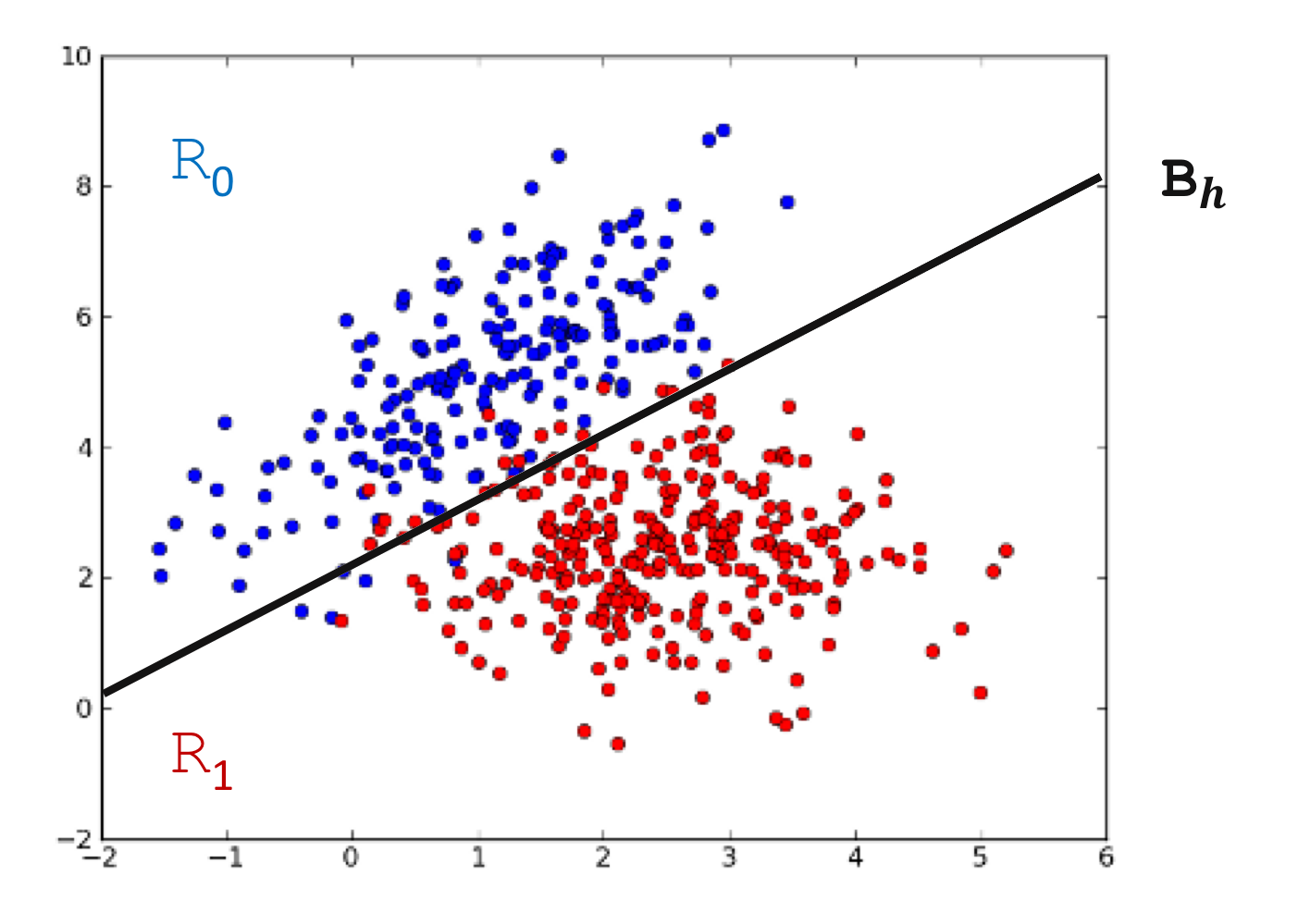
2차원 데이터의 선형 분류

• 선형 판별 함수(Linear Discriminant Function): 클래스 분류의 기준이 될 수 있는 판별 함수(Discriminant Function)가 선형적이다. $$h: \mathbb {R}^n \rightarrow \mathbb {R}, \mathbf {x} \mapsto \mathbf {w}^{\top} \mathbf {x} + w_0$$
• 분류 규칙(Classification Rule): $$y = \begin {cases} 1 & h(\mathbf {x}) \geq 0 \\ 0 & h(\mathbf {x}) < 0 \end {cases}$$
• 결정 경계(Decision Boundary): $$\mathcal {B}_h = \{\mathbf {x} \in \mathbb {R}^n: h(\mathbf {x}) = 0 \}$$
• 클래스 영역(Class Regions): $$R_1 = \{ \mathbf {x}: h(\mathbf {x}) \geq 0 \}, R_0 = \{\mathbf {x}: h(\mathbf {x}) < 0 \}$$

  ---

아래의 그림은 3차원 데이터의 2차원 선형면으로 분류하는 자세한 예를 보여준다.

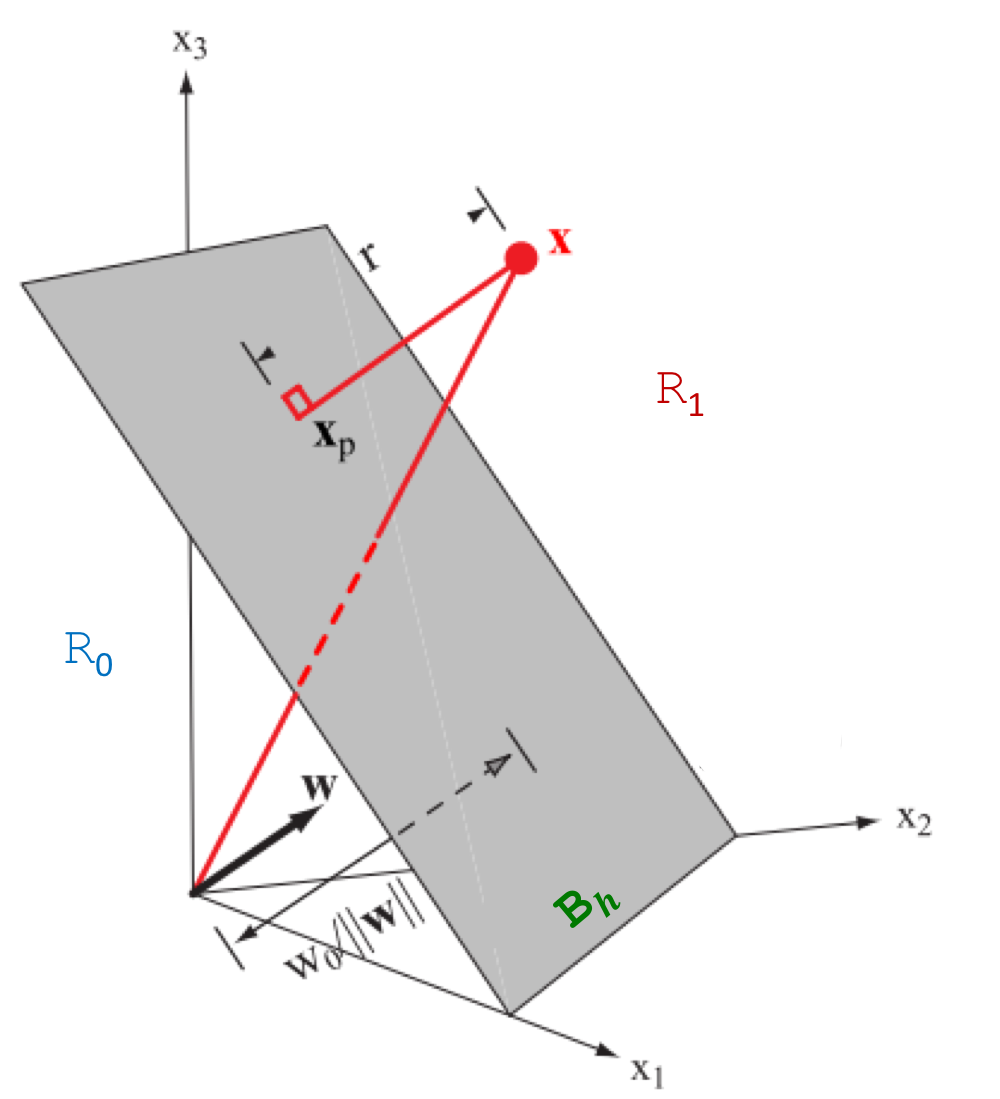
3차원 데이터의 선형 분류

• 선형 판별 함수: $$h(\mathbf {x}) = w_0 + w_1 x_1 + w_2 x_2$$
• 결정 경계: $$\mathcal {B}_h = \{\mathbf {x} \in \mathbb {R}^2: h(\mathbf {x}) = 0 \}$$

3차원 데이터 $\mathbf {x}$에서부터 초평면(Hyperplane) $\mathcal {B}_h$ 위에 정사영(Orthographic Projection)된 점 $\mathbf {x}_p$ 의 거리 $r$을 계산해서 $R_0$ 혹은 $R_1$로 분류한다.

점 $(x_0, y_0, z_0)$과 평면 $ax + by + cz + d = 0$의 거리 $d(점, 평면)$:
$$d(점, 평면) = \frac {|ax_0 + by_0 + cz_0 +d|}{\sqrt {a^2 + b^2 + c^2}}$$

• 원점 (0, 0, 0)과 초평면까지의 최소 거리: $$r_0 = d(0, \mathcal {B}_h) = \frac {|w_0 + w_1 \cdot 0 + w_2 \cdot 0|}{\sqrt {w_0^2 + w_1^2 + w_2^2}}= \frac {w_0}{||\mathbf {w}||}$$
• $\mathbf {x}$와 초평면에 정 사영된 $\mathbf {x}_p$의 거리(※ 양수 혹은 음수): $$r = d(\mathbf {x}, \mathcal {B}_h) = \frac {w_0 + w_1x_1 + w_2x_2}{\sqrt {w_0^2 + w_1^2 + w_2^2}} = \frac {h(\mathbf {x})}{||\mathbf {w}||}$$

위에서처럼 학습 데이터(Training Data)를 초평면에 정사 영시 킨 후, 그 거리의 부호를 구하면 이진 분류(Binary Classification)가 가능하다.

※ 증명

---

 

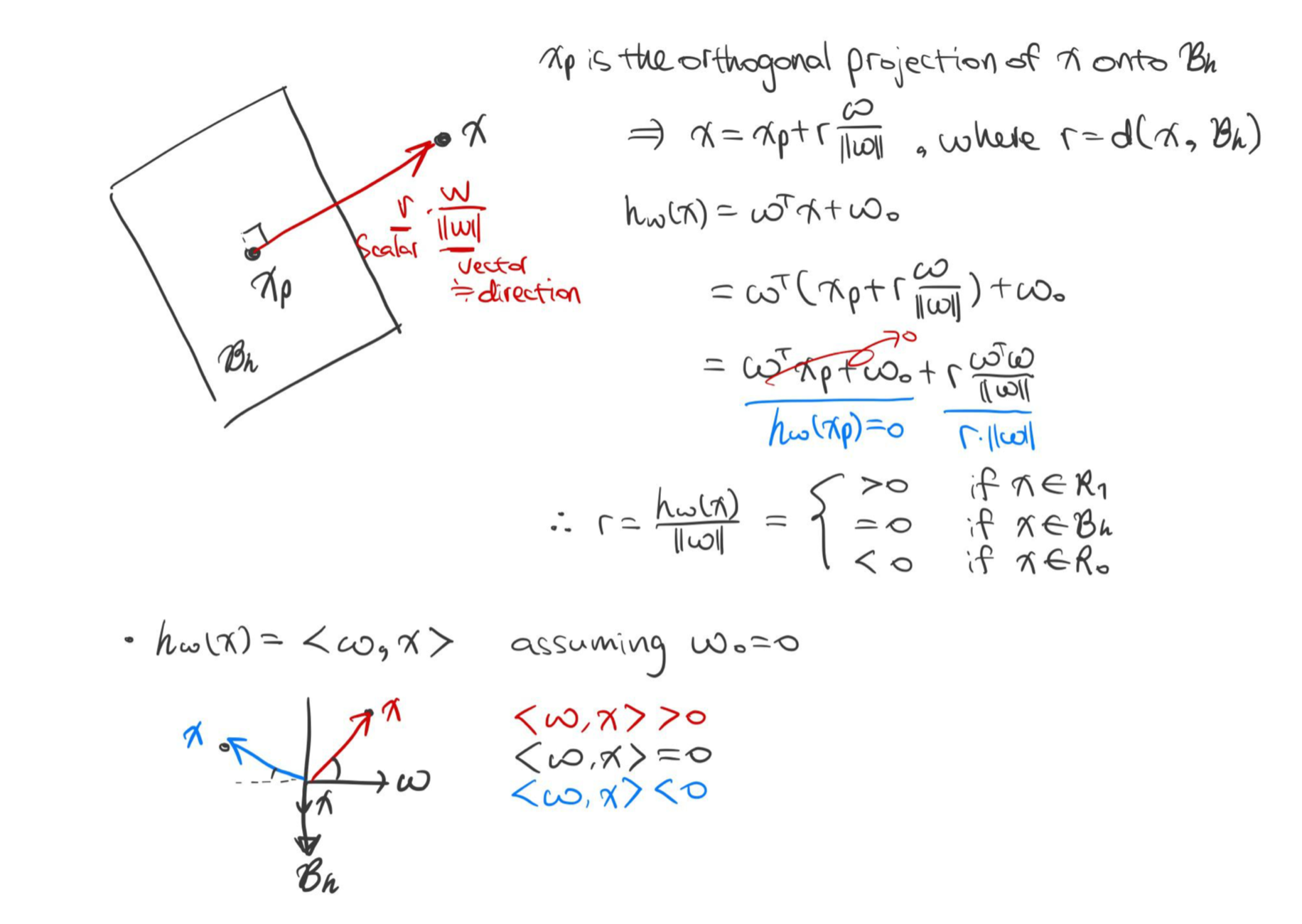
※ $\mathbf {w} \perp \mathcal {B}_h$ 증명

---

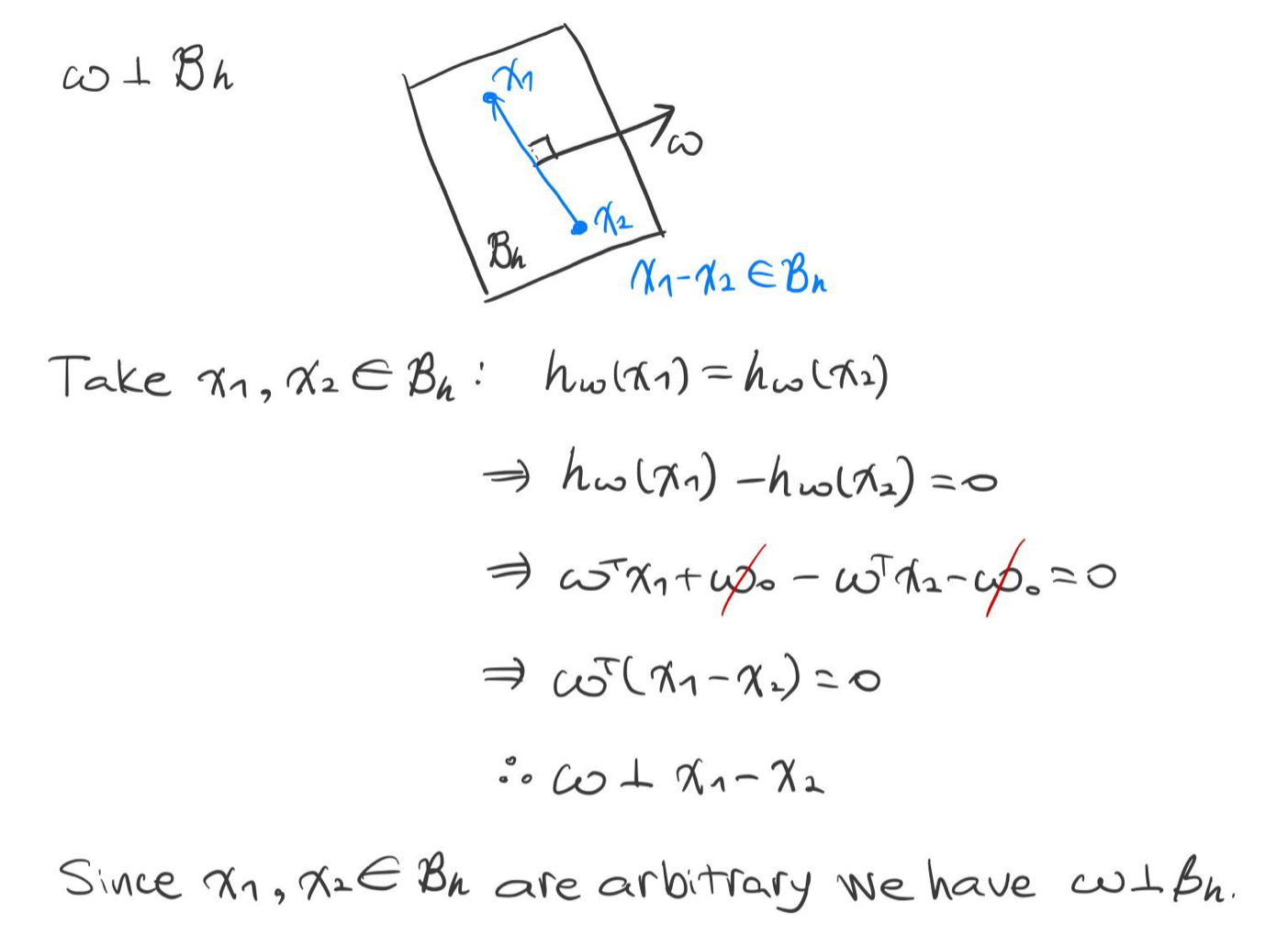
경험적 위험도 최소화(Empirical Risk Minimization)

이렇게 분류한 모델이 잘 분류되었는지 판단하려면 어떤 기준점이 필요한데, 이를 위해 경험적 위험도 최소화(ERM) 방법을 사용한다. ERM의 핵심은 다음과 같다.

분류 결과에 대한 손실 함수(Loss Function)를 설정해 잘못 분류됐을 경우 페널티(Penalty)를 부여 → 각 예측된 분류 결과에 대한 기대 손실 값인 기대 위험도를 최소화(Expected Risk Minimization) → 학습 데이터만으로 기대 위험도를 구할 수 없으니 경험적 위험도를 대신 최소화

---

손실 함수(Loss Function)

손실 함수 $\phi(\hat {y}, y)$는 $y$ 클래스로 분류되어야 할 데이터가 $\hat {y}$ 클래스로 잘못 분류됐을 때 발생하는 비용을 말한다.

※ 손실 함수의 종류 자료

[Machine Learning] 베이즈 결정 이론(Bayesian Decision Theory)

Q. ERM에서 제로-원 손실 함수(Zero-One Loss Function)가 적합하지 않은 이유는?
A. 제로-원 손실 함수는 불연속 계단 함수(Discontinuous Step Function)로 비 볼록 함수(Non-Convex Function)이기도 하다. 따라서 제로-원 손실을 이용한 ERM은 NP-난해(NP-Hard) 문제이며, 미분을 이용한 해결 방식인 경사 하강법(Gradient Descent)을 적용할 수가 없다.

---

예 1) 로지스틱 손실(Logistic Loss)

$$\phi(\hat {y}, y) = \log (1 + \exp (-y \hat {y}))$$

아래의 그래프는 (a) 제로-원 손실, (b) 제곱 손실(Squared Loss) (c) 로지스틱 손실에 대한 경험적 위험도를 도면화하였다. 제곱 손실과 로지스틱 손실은 아래가 완만한 반면 제로-원 손실은 계단 함수 형태를 보여준다.

 

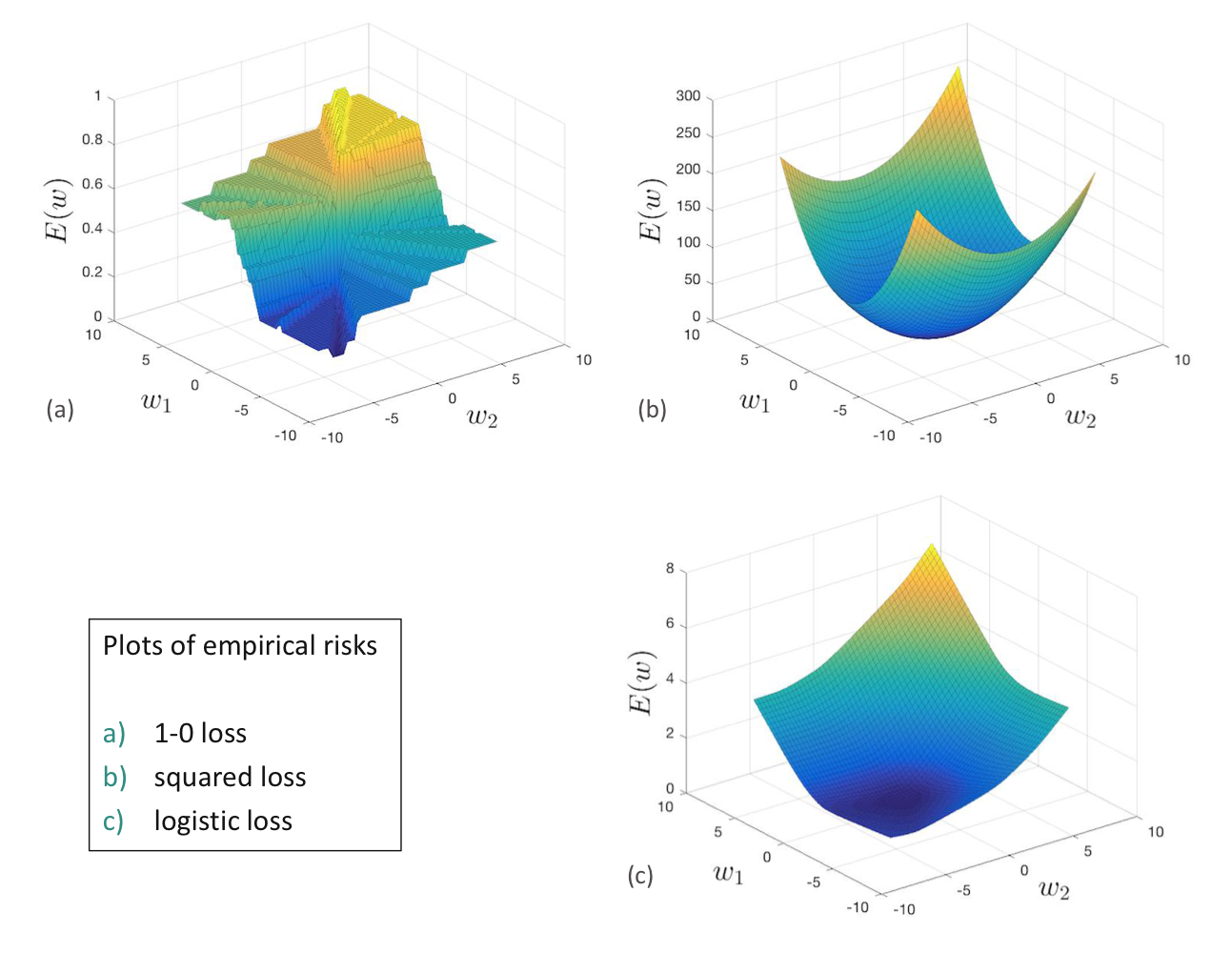
세가지 손실 함수에 대한 경험적 위험도

---

대리 손실 함수(Surrogate Loss Function)

Q. 기대 위험도 최소화 대신 ERM을 사용할 수 있는 경우는?
A. 손실 함수 $\phi$이 볼록(Convex)하고, $0$에서 미분 가능하며, $\phi'(0) < 0$인 경우를 
피셔의 일치성(Fisher Consistency)이라고 하며, 이가 만족되어야 ERM으로 기대 위험도 취소화를 대신할 수 있다.

피셔의 일치성(Fisher Consistency):
$E^*_l = \min E_l [h]$와 $E^*_\phi = \min E_\phi [h]$를 베이즈 위험도(Bayes Risk)라고 하자. 대리 손실 함수 $\phi$가 다음 조건에서 피셔의 일치성을 만족한다.
For any sequence $(h_n)$ of functions $E^*_\phi [h_n] \rightarrow E^*_\phi$ implies $E^*_l [h_n] \rightarrow E^*_l$

피셔의 일치성으로 제로-원 손실 함수는 적합하지 않음을 다시 한번 확인할 수 있다.

---

ERM의 구체적인 예시

※ 참고

$m$	학습 세트의 개수(Number of training examples)
$n$	특성의 개수(Number of features)
$y \in \mathcal{Y} = \{0, 1\}$	클래스 레이블(Class labels)
$w = (w_0, w_1,..., w_n)$	모수 벡터(Parameter Vector)
$x = (1, x_1, ..., x_n)$	증강된 특성 벡터(Augmented Feature Vector)

ERM: 아래의 조건에서 경험적 위험도 $J(w) = \sum^m_{i = 1} l(h_w(x_i), y_i)$를 최소화하여라.

• 학습 세트(Training Set) $(x_1, y_1), (x_2, y_2),..., (x_m, y_m) \in \mathbb {R}^{n+1} \times \mathrm {Y}$
• 가설 공간(Hypothesis Space) $\mathrm {H}$ of linear functions $h: \mathbb {R}^{n+1} \rightarrow \mathbb {R}$
• 볼록 손실 함수(Convex Loss Function) $l: \mathbb {R} \times \mathrm {Y} \rightarrow \mathbb {R}$

  ---

예 1) 일반화된 ERM

• 일반화된 손실 함수(General Loss Function) $$l(\hat {y}, y)$$
• 경험적 위험도 $$J(w) = \frac {1}{m} \sum^m_{i = 1} l(h_w(x_i), y_i)$$
• 경사 하강법 종료 시까지 반복 $$w_j \leftarrow w_j - \eta \frac {\partial}{\partial w_j} J(w) \text { for all } j$$

  ---

예 2) 선형 회귀(Linear Regression)

• 제곱 손실 함수 $$\phi(\hat {y}, y) = (\hat {y} - y)^2, \text { where } y \in \{0, 1\}$$
• 경험적 위험도 $$J(w) = \frac {1}{2m} \sum^m_{i = 1} (h_w(x_i) - y_i)^2$$
• 경사 하강법 종료 시까지 반복 $$w_j \leftarrow w_j - \frac {\eta}{m} \sum^m_{i = 1} (h_w(x_i) - y_i) x_{ij} \text { for all } j$$

  ---

예 3) 로지스틱 회귀(Logistic Regression)

• 로지스틱 손실 함수 $$\phi(\hat {y}, y) = \log (1 + \exp (- \hat {y} y)), \text { where } y \in \{\pm 1\}$$
• 경험적 위험도 $$J(w) = \frac {1}{m} \sum^m_{i = 1} \log (1 + \exp (-y_i \cdot h_w(x_i)))$$
• 경사 하강법 종료 시까지 반복 $$w_j \leftarrow w_j + \frac {\eta}{m} \sum^m_{i = 1} \frac {y_i \cdot x_{ij}}{1 + \exp (y_i \cdot h_w(x_i))} \text { for all } j$$

※ 로지스틱 회귀의 증명

※ 로지스틱 회귀의 또 다른 표현법. (두 식에서 가질 수 있는 클래스의 값이 다르다.)

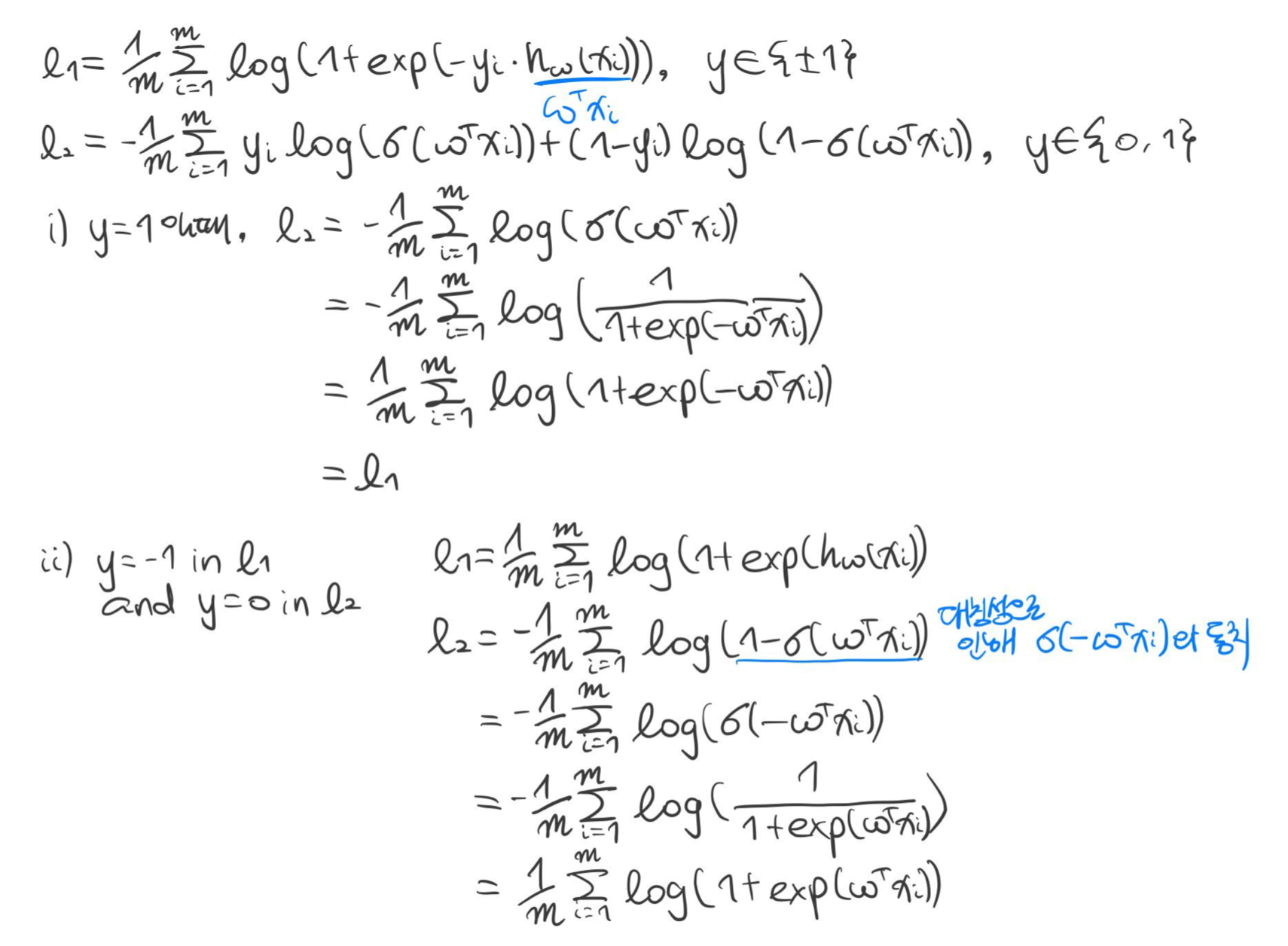
※ 로지스틱 회귀의 확률적 해석

---

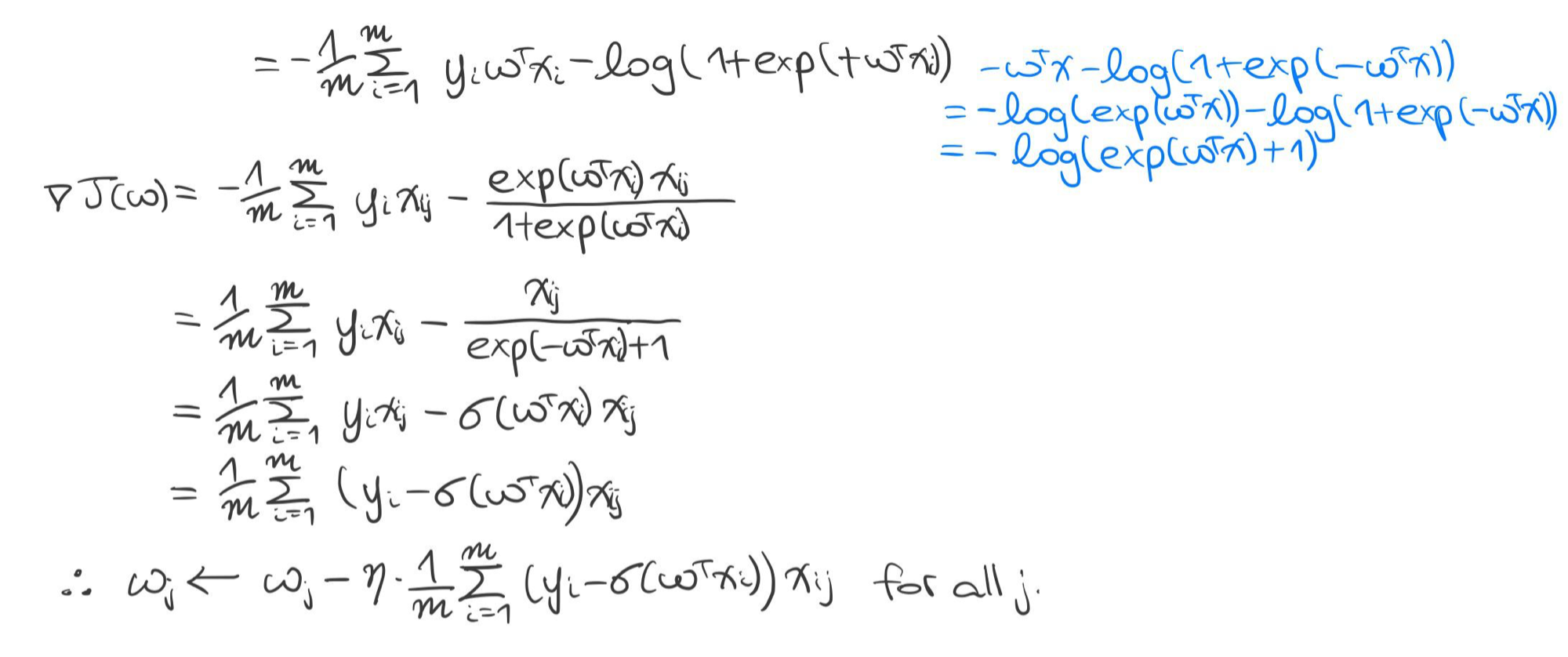
※ [Machine Learning] 퍼셉트론 인공신경망(Perceptron Artificial Neural Network)

[Machine Learning] 퍼셉트론 인공신경망(Perceptron Artificial Neural Network)

※ [Machine Learning] 피셔의 선형 판별 분석(Fisher Linear Discriminant Analysis)

[Machine Learning] 피셔의 선형 판별 분석(Fisher Linear Discriminant Analysis)

---

1. Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification (2nd Edition). Wiley-Interscience, USA.