[Machine Learning] 선형 분류(Linear Classification)

선형 분류는 일차원 혹은 다차원 데이터들을 선형 모델(Linear Model)을 이용하여 클래스들로 분류(Classification)하는 머신러닝(Machine Learning) 기법이다. 아래 예시는 2차원 데이터를 어떤 선형 모델로 $R_0$ 혹은 $R_1$로 분류하는 선형 분류를 보여준다.

2차원 데이터의 선형 분류

• 선형 판별 함수(Linear Discriminant Function): 클래스 분류의 기준이 될 수 있는 판별 함수(Discriminant Function)가 선형적이다. $$h:{\mathbb{R}}^n\to \mathbb{R},\mathbf{x}\mapsto {\mathbf{w}}^{\mathrm{\top }}\mathbf{x}+w_0$$
• 분류 규칙(Classification Rule): $$y=\{\begin{array}{ll}1& h(\mathbf{x})\ge 0\\ 0& h(\mathbf{x})<0\end{array}$$
• 결정 경계(Decision Boundary): $${\mathcal{B}}_h=\{\mathbf{x}\in {\mathbb{R}}^n:h(\mathbf{x})=0\}$$
• 클래스 영역(Class Regions): $$R_1=\{\mathbf{x}:h(\mathbf{x})\ge 0\},R_0=\{\mathbf{x}:h(\mathbf{x})<0\}$$

  ---

아래의 그림은 3차원 데이터의 2차원 선형면으로 분류하는 자세한 예를 보여준다.

3차원 데이터의 선형 분류

• 선형 판별 함수: $$h(\mathbf{x})=w_0+w_1{x}_1+w_2{x}_2$$
• 결정 경계: $${\mathcal{B}}_h=\{\mathbf{x}\in {\mathbb{R}}^2:h(\mathbf{x})=0\}$$

3차원 데이터 $\mathbf{x}$에서부터 초평면(Hyperplane) ${\mathcal{B}}_h$ 위에 정사영(Orthographic Projection)된 점 ${\mathbf{x}}_p$ 의 거리 $r$을 계산해서 $R_0$ 혹은 $R_1$로 분류한다.

점 $(x_0,y_0,z_0)$과 평면 $ax+by+cz+d=0$의 거리 $d(점,평면)$:
$$d(점,평면)=\frac{|a{x}_0+b{y}_0+c{z}_0+d|}{\sqrt{a^2+b^2+c^2}}$$

• 원점 (0, 0, 0)과 초평면까지의 최소 거리: $$r_0=d(0,{\mathcal{B}}_h)=\frac{|w_0+w_1\cdot 0+w_2\cdot 0|}{\sqrt{w_0^2+w_1^2+w_2^2}}=\frac{w_0}{||\mathbf{w}||}$$
• $\mathbf{x}$와 초평면에 정 사영된 ${\mathbf{x}}_p$의 거리(※ 양수 혹은 음수): $$r=d(\mathbf{x},{\mathcal{B}}_h)=\frac{w_0+w_1{x}_1+w_2{x}_2}{\sqrt{w_0^2+w_1^2+w_2^2}}=\frac{h(\mathbf{x})}{||\mathbf{w}||}$$

위에서처럼 학습 데이터(Training Data)를 초평면에 정사 영시 킨 후, 그 거리의 부호를 구하면 이진 분류(Binary Classification)가 가능하다.

※ 증명

---

 

※ $\mathbf{w}\perp {\mathcal{B}}_h$ 증명

---

경험적 위험도 최소화(Empirical Risk Minimization)

이렇게 분류한 모델이 잘 분류되었는지 판단하려면 어떤 기준점이 필요한데, 이를 위해 경험적 위험도 최소화(ERM) 방법을 사용한다. ERM의 핵심은 다음과 같다.

분류 결과에 대한 손실 함수(Loss Function)를 설정해 잘못 분류됐을 경우 페널티(Penalty)를 부여 → 각 예측된 분류 결과에 대한 기대 손실 값인 기대 위험도를 최소화(Expected Risk Minimization) → 학습 데이터만으로 기대 위험도를 구할 수 없으니 경험적 위험도를 대신 최소화

---

손실 함수(Loss Function)

손실 함수 $\varphi (\hat{y},y)$는 $y$ 클래스로 분류되어야 할 데이터가 $\hat{y}$ 클래스로 잘못 분류됐을 때 발생하는 비용을 말한다.

※ 손실 함수의 종류 자료

[Machine Learning] 베이즈 결정 이론(Bayesian Decision Theory)

Q. ERM에서 제로-원 손실 함수(Zero-One Loss Function)가 적합하지 않은 이유는?
A. 제로-원 손실 함수는 불연속 계단 함수(Discontinuous Step Function)로 비 볼록 함수(Non-Convex Function)이기도 하다. 따라서 제로-원 손실을 이용한 ERM은 NP-난해(NP-Hard) 문제이며, 미분을 이용한 해결 방식인 경사 하강법(Gradient Descent)을 적용할 수가 없다.

---

예 1) 로지스틱 손실(Logistic Loss)

$$\varphi (\hat{y},y)=\log (1+\exp (-y\hat{y}))$$

아래의 그래프는 (a) 제로-원 손실, (b) 제곱 손실(Squared Loss) (c) 로지스틱 손실에 대한 경험적 위험도를 도면화하였다. 제곱 손실과 로지스틱 손실은 아래가 완만한 반면 제로-원 손실은 계단 함수 형태를 보여준다.

 

세가지 손실 함수에 대한 경험적 위험도

---

대리 손실 함수(Surrogate Loss Function)

Q. 기대 위험도 최소화 대신 ERM을 사용할 수 있는 경우는?
A. 손실 함수 $\varphi$이 볼록(Convex)하고, $0$에서 미분 가능하며, ${\varphi }^{\prime }(0)<0$인 경우를 
피셔의 일치성(Fisher Consistency)이라고 하며, 이가 만족되어야 ERM으로 기대 위험도 취소화를 대신할 수 있다.

피셔의 일치성(Fisher Consistency):
$E_l^{\ast }=min{E}_l[h]$와 $E_{\varphi }^{\ast }=min{E}_{\varphi }[h]$를 베이즈 위험도(Bayes Risk)라고 하자. 대리 손실 함수 $\varphi$가 다음 조건에서 피셔의 일치성을 만족한다.
For any sequence $(h_n)$ of functions $E_{\varphi }^{\ast }[h_n]\to E_{\varphi }^{\ast }$ implies $E_l^{\ast }[h_n]\to E_l^{\ast }$

피셔의 일치성으로 제로-원 손실 함수는 적합하지 않음을 다시 한번 확인할 수 있다.

---

ERM의 구체적인 예시

※ 참고

$m$	학습 세트의 개수(Number of training examples)
$n$	특성의 개수(Number of features)
$y\in \mathcal{Y}=\{0,1\}$	클래스 레이블(Class labels)
$w=(w_0,w_1,...,w_n)$	모수 벡터(Parameter Vector)
$x=(1,x_1,...,x_n)$	증강된 특성 벡터(Augmented Feature Vector)

ERM: 아래의 조건에서 경험적 위험도 $J(w)=\sum _{i=1}^{m}l(h_w(x_i),y_i)$를 최소화하여라.

• 학습 세트(Training Set) $(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\in {\mathbb{R}}^{n+1}\times \mathrm{Y}$
• 가설 공간(Hypothesis Space) $\mathrm{H}$ of linear functions $h:{\mathbb{R}}^{n+1}\to \mathbb{R}$
• 볼록 손실 함수(Convex Loss Function) $l:\mathbb{R}\times \mathrm{Y}\to \mathbb{R}$

  ---

예 1) 일반화된 ERM

• 일반화된 손실 함수(General Loss Function) $$l(\hat{y},y)$$
• 경험적 위험도 $$J(w)=\frac{1}{m}\sum _{i=1}^{m}l(h_w(x_i),y_i)$$
• 경사 하강법 종료 시까지 반복 $$w_j\leftarrow w_j-\eta \frac{\partial }{\partial w_j}J(w)\text{ for all }j$$

  ---

예 2) 선형 회귀(Linear Regression)

• 제곱 손실 함수 $$\varphi (\hat{y},y)=(\hat{y}-y{)}^2,\text{ where }y\in \{0,1\}$$
• 경험적 위험도 $$J(w)=\frac{1}{2m}\sum _{i=1}^m(h_w(x_i)-y_i{)}^2$$
• 경사 하강법 종료 시까지 반복 $$w_j\leftarrow w_j-\frac{\eta }{m}\sum _{i=1}^m(h_w(x_i)-y_i)x_{ij}\text{ for all }j$$

  ---

예 3) 로지스틱 회귀(Logistic Regression)

• 로지스틱 손실 함수 $$\varphi (\hat{y},y)=\log (1+\exp (-\hat{y}y)),\text{ where }y\in \{\pm 1\}$$
• 경험적 위험도 $$J(w)=\frac{1}{m}\sum _{i=1}^m\log (1+\exp (-y_i\cdot h_w(x_i)))$$
• 경사 하강법 종료 시까지 반복 $$w_j\leftarrow w_j+\frac{\eta }{m}\sum _{i=1}^m\frac{y_i\cdot x_{ij}}{1+\exp (y_i\cdot h_w(x_i))}\text{ for all }j$$

※ 로지스틱 회귀의 증명

※ 로지스틱 회귀의 또 다른 표현법. (두 식에서 가질 수 있는 클래스의 값이 다르다.)

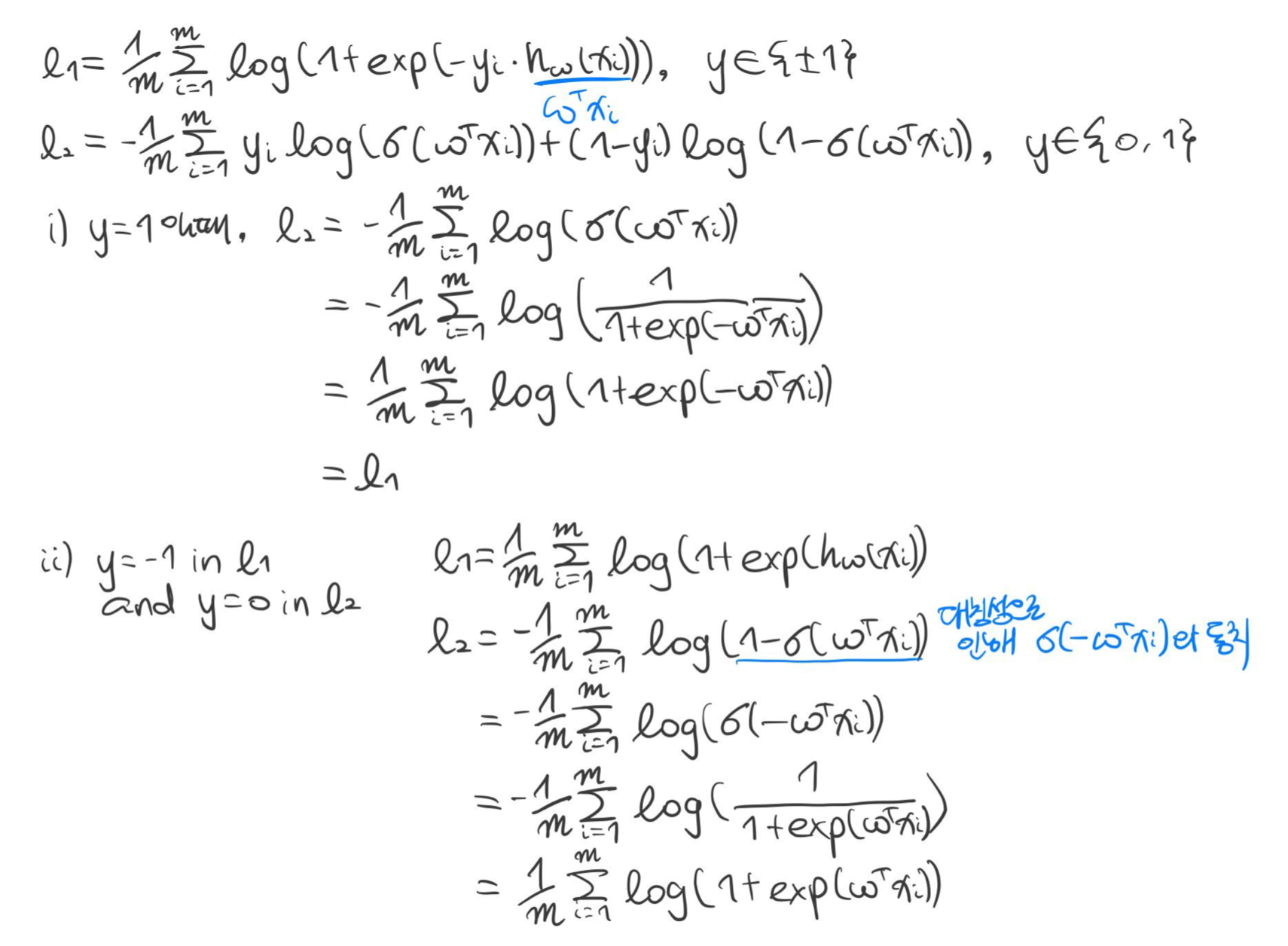
※ 로지스틱 회귀의 확률적 해석

---

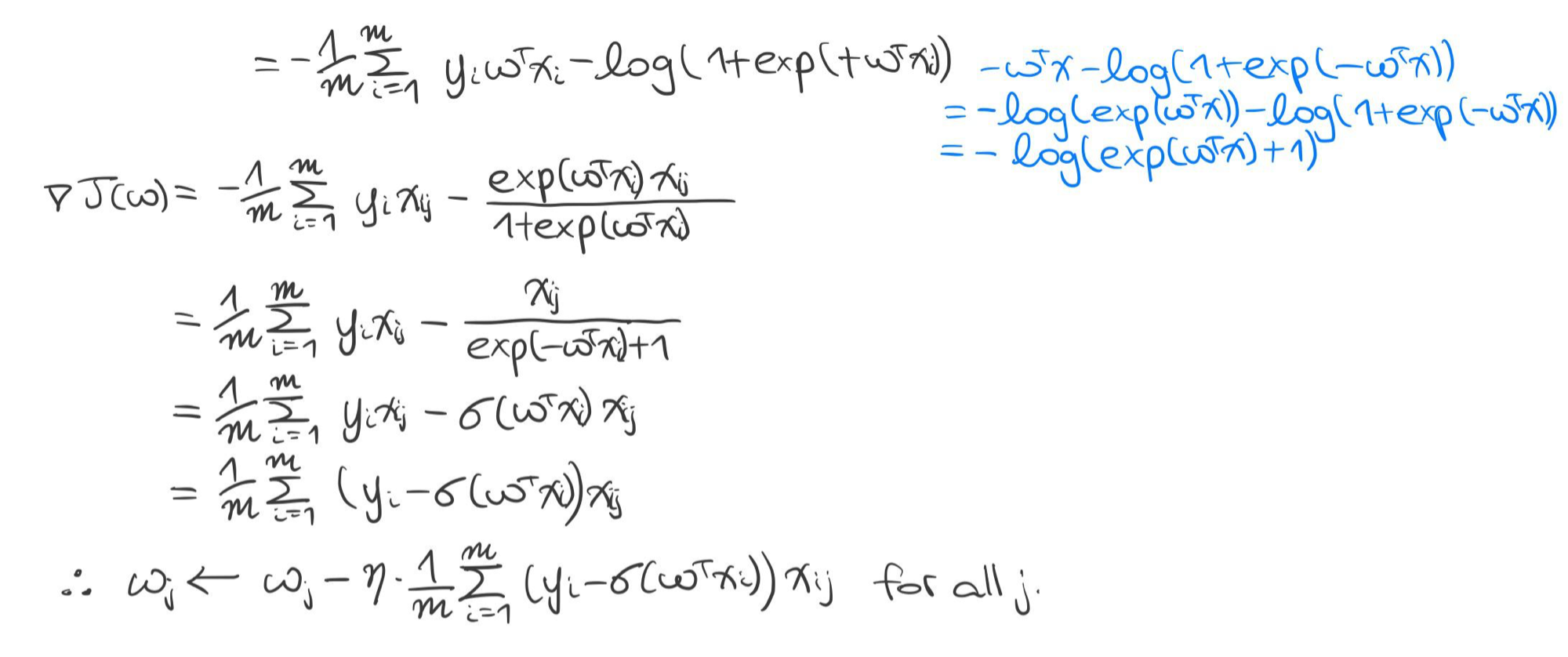
※ [Machine Learning] 퍼셉트론 인공신경망(Perceptron Artificial Neural Network)

[Machine Learning] 퍼셉트론 인공신경망(Perceptron Artificial Neural Network)

※ [Machine Learning] 피셔의 선형 판별 분석(Fisher Linear Discriminant Analysis)

[Machine Learning] 피셔의 선형 판별 분석(Fisher Linear Discriminant Analysis)

---

1. Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification (2nd Edition). Wiley-Interscience, USA.