[Machine Learning] 상관계수(Correlation Coefficient)

상관계수는 두 변수 사이의 통계적 관계를 표현하기 위해 특정한 상관관계의 정도를 수치적으로 나타낸 계수이다. [wikipedia]

---

$\mathbf {x}_t \in \mathbb {R}^{T \times 1}$과 $\mathbf {y} \in \mathbb {R}^{T \times 1}$가 주어졌을 때, $\mathbf {x}$과 $\mathbf {y}$의 상관계수의 경험적 추정치는 다음과 같다.

$$
\begin {align*}
Corr(\mathbf {x}, \mathbf {y}) &= \sum_t \frac {x_t y_t}{\sqrt {x^2_t y^2_t}} \\
&= \frac {\mathbf {x}^{\top} \mathbf {y}}{\sqrt {\mathbf {x}^{\top} \mathbf {x} \mathbf {y}^{\top} \mathbf {y}}}
\end {align*}
$$

$$\text {where we assume centered data, i.e. } \sum^T_{t = 1} x_t = \sum^T_{t = 1} y_t = 0$$

상관계수는 반드시 -1과 1 사이에 위치한다. -1에 가까울 수록 음의 상관관계, 1에 가까울 수록 양의 상관관계를 의미한다. 상관계수가 0일 때, 두 변수는 상관관계가 없다고 간주한다.

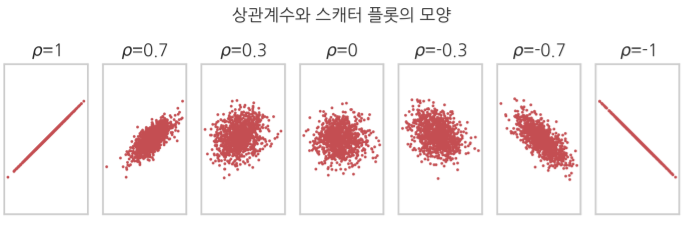
출처: https://velog.io/@tonyhan18/7.5-공분산과-상관계수