-
[Machine Learning] 공분산 행렬(Covariance Matrix)Informatik 2022. 2. 16. 20:11
교차 공분산 행렬(Cross Covariance Matrix)
확률 변수(Random Variable) $X, Y$의 평균이 각각 $\mu_X, \mu_Y$일 때, 교차 공분산 행렬 $\Sigma$은 다음과 같이 정의된다.
$$Cov (X, Y) = \mathbb {E} [(X- \mu_X)(Y - \mu_Y)^{\top}]$$
공분산 행렬(Covariance Matrix)
일반적인 공분산 행렬
확률 변수(Random Variable) $X$의 평균이 $\mu$일 때, 공분산 행렬은 다음과 같이 정의된다.
$$Var (X) = Cov (X) = \mathbb {E} [(X- \mu)(X - \mu)^{\top}]$$
정렬된 데이터의 공분산 행렬
$T$개의 데이터 $\mathbf {x} \in \mathbb {R}^D$로 구성된 행렬 $\mathbf {X} \in \mathbb {R}^{D \times T}$가 주어졌을 때, 공분산 행렬의 경험적 추정치는 다음과 같이 정의된다.
$$\frac {1}{T} \mathbf {X} \mathbf {X}^{\top}, \text { where we assume centered data, i.e. } \sum^T_{t = 1} x_t = 0$$
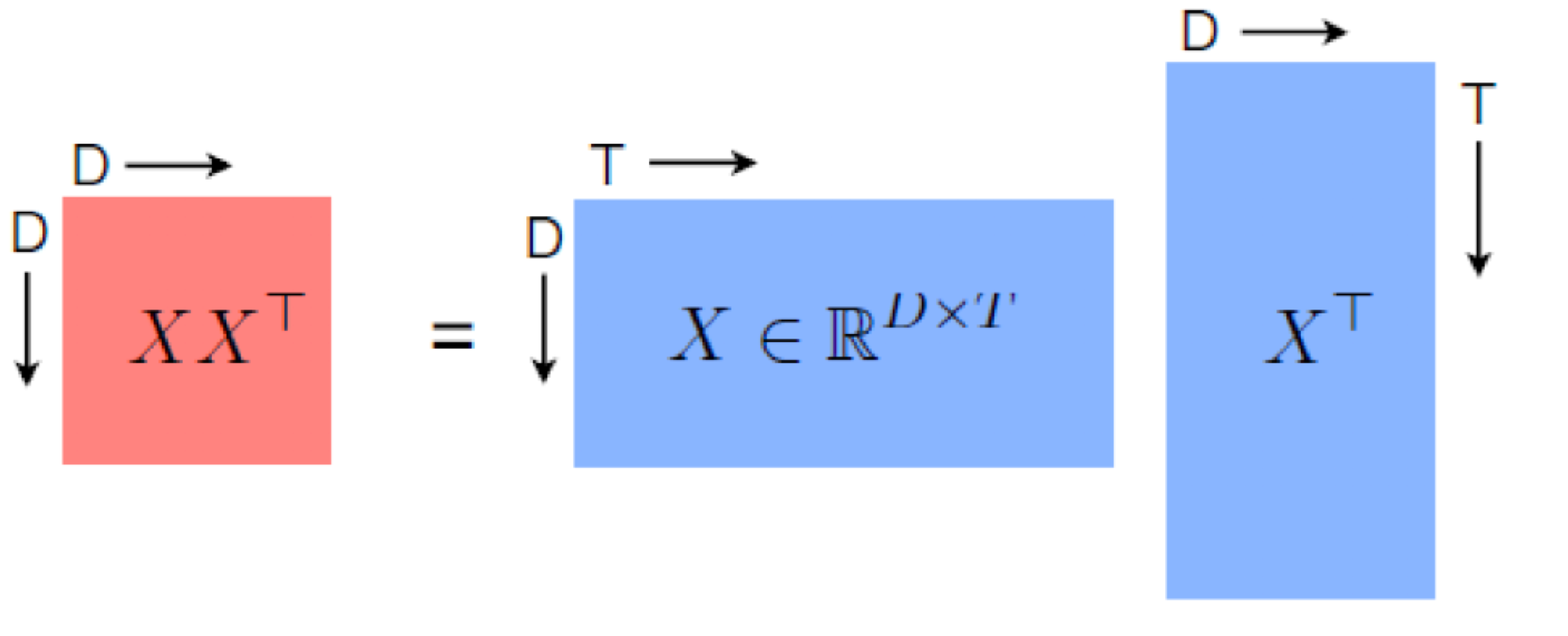
'Informatik' 카테고리의 다른 글
[Machine Learning] 인공 신경망(Artificial Neural Network) (0) 2022.02.18 [Machine Learning] 피셔의 선형 판별 분석(Fisher Linear Discriminant Analysis) (5) 2022.02.17 [Machine Learning] 상관계수(Correlation Coefficient) (0) 2022.02.16 [Machine Learning] 퍼셉트론 인공신경망(Perceptron Artificial Neural Network) (0) 2022.02.16 [Machine Learning] NCC(Nearest Centroid Classifier) (0) 2022.02.16