[Machine Learning] 나이브 베이즈 분류(Naïve Bayes Classification)

※ 나이브 베이즈 분류(Naive Bayes Classification)를 공부하기 전에 베이즈 결정 이론(Bayesian Decision Theory)에 대한 기초 지식이 없다면 밑에 링크를 통해 먼저 공부하고 오는 것을 추천합니다.

※ [Machine Learning] 베이즈 결정 이론(Bayesian Decision Theory)

[Machine Learning] 베이즈 결정 이론(Bayesian Decision Theory)

---

서론

베이즈 분류는 특징(Feature)의 종류와 차원이 증가할수록 계산해야 할 우도(Likelihood)의 경우의 수가 다양해져 모델이 더 복잡해진다. 예를 들어, 총 특징의 개수 $n$과 임의의 이진 특징 벡터(Binary Feature Vector) $\mathbf {x}_i$가 주어졌을 때, 베이즈 분류를 적용해 $c$ 개의 레이블로 분류한다고 가정하자. 이 때, 특징 벡터 $\mathbf {x}_i$의 경우의 수는 $2^n$ 이다. 베이즈 분류를 적용하기 위해서는 우도 $P(\mathbf {x}_i | y_k)$를 구해야 하는데 (임의의 레이블 $y_k$), 우도를 구하는 계산 복잡도는 $\mathcal {O} (c \cdot 2^n)$이다.

• 특징의 종류가 증가하는 경우 ($n$이 증가하는 경우) → 우도를 구하는 계산 복잡도가 기하급수적으로 증가한다.
• 특징의 차원이 증가하는 경우 (이진 특징 벡터가 아닌, 특징이 $m$ 개의 다른 값을 갖는 특징 벡터의 경우) → 우도를 구하는 계산 복잡도는 $\mathcal {O} (c \cdot m^n)$로, 이 또한 증가한다.

따라서, 특징의 종류와 차원이 매우 큰 경우, 베이즈 분류를 사용하는 것은 바람직하지 않다. 이를 위한 대안으로, 나이브 베이즈 분류기로 조건부 독립(Conditional Independece)을 활용해 우도의 계산 복잡도를 $\mathcal {O} (c \cdot 2^n)$에서 $\mathcal {O} (c n)$까지 줄일 수 있다.

---

나이브 베이즈 분류기(Naīve Bayes Classifier)

나이브 베이즈 분류를 다음과 같은 예제로 이해해보자. 우선 다음과 같이 입력 공간(Input Space), 클래스 레이블(Class Label), 학습 데이터세트(Training Set)를 표기한다고 가정하자. 

• 입력 공간 $\mathbf {X} \subseteq \mathbb {R}$
• 클래스 레이블 $\mathbf {Y} = \{ 1, \cdots, c\}$
• 학습 데이터세트 $(\mathbf {x}_1, y_1), \cdots, (\mathbf {x}_m, y_m) \in \mathbf {X}^n \times \mathbf {Y}$

※ 참고

특정 요소를 지칭할 때		벡터를 지칭할 때
$y_i$	$i$ 번째 클래스 레이블($i$-th Class Label)	$y$	클래스 레이블(Class Label)
$\mathbf {x}_i$	$i$ 번째 특징 벡터($i$-th Feature Vector)	$\mathbf {x}$	특징 벡터(Feature Vector)
$x_{ij}$	$x_i$의 $j$ 번째 특징($j$-th Feature of $x_i$)	$x_j$	$j$ 번째 특징($j$-th Feature)

---

※ 필수 명제 및 이론 정리

베이즈 이론(Bayes Theory):
$$P(A | B) = \frac {P(B | A) P(A)}{P(B)}$$

조건부 확률(Conditional Probability):
$$P(A | B) = \frac {P(A, B)}{P(B)}$$

조건부 독립(Conditional Independence):
특징 $\mathbf {x}$와 $\mathbf {x}'$가 레이블 $y$가 주어졌을 때, 다음의 식이 만족할 때, 조건부 독립이다.
$$P(\mathbf {x}, \mathbf {x}' | y) = P(\mathbf {x} | y) P (\mathbf {x}'| y)$$

조건부 독립성을 이용하면 다음과 같이 결합 확률(Joint Probability)을 정리할 수 있다.
$\text {According to the definition of conditional probability,}$
$$\begin {align*}
p(C_k, x_1, \cdots, x_n) &= p(x_1, \cdots, x_n, C_k) \\
&= p(x_1 | x_2, \cdots, x_n, C_k) p(x_2, \cdots, x_n, C_k) \\
&= p(x_1 | x_2, \cdots, x_n, C_k) p(x_2 | x_3, \cdots, x_n, C_k) p(x_3, \cdots, x_n, C_k) \\
&= \cdots \\
&= p(x_1 | x_2, \cdots, x_n, C_k) p(x_2 | x_3, \cdots, x_n, C_k) \cdots p(x_{n - 1} | x_n, C_k) p(x_n | C_k) p (C_k)
\end {align*}$$
$$\begin{align*}
\text {Assuming Conditional Independence, } \\
&= p(x_1 | C_k) p(x_2 | C_k) \cdots p(x_{n - 1} | C_k) p(x_n | C_k) p (C_k) 
\end {align*}$$
$\text {Using Bayes Theorem,}$
$$\begin {align*}
p(C_k | x_1, \cdots, x_n) &= \frac {p(x_1, \cdots, x_n | C_k) P(C_k)}{p(x_1, \cdots, x_n)} \\
&= \frac {p(x_1, \cdots, x_n, C_k)}{p(x_1, \cdots, x_n)} \\
&= \frac {p(C_k, x_1, \cdots, x_n)}{p(x_1, \cdots, x_n)} \\ \\
\therefore p(C_k | x_1, \cdots, x_n) &\propto p(C_k, x_1, \cdots, x_n) \\
&\propto p(C_k) p(x_1 | C_k) p(x_2 | C_k) p(x_3 | C_k) \cdots \\
&\propto p(C_k) \prod^n_{i = 1} p(x_i | C_k)
\end {align*}$$

---

어떤 특징 벡터 $\mathbf {x} = (x_1, \cdots, x_n) \in \mathbf {X}^n$를 나이브 베이즈 분류를 하려고 한다. 이때 계산의 편의성을 위해, 모든 특징들은 서로 조건부 독립이라고 가정한다.
$$p(\mathbf {x} | y) = \prod^n_{j = 1} p(x_j | y)$$
나이브 베이즈 분류기는 다음과 같다. (※ MAP을 이용한 분류기)
$$h(x) = arg \max_{k \in \mathbf {Y}} P(y_k) \prod^n_{j = 1} p(x_j | y_k)$$
프로그래밍 시 오버플로우(Overflow) 방지를 위해 나이브 베이즈 분류기에 로그를 적용하면 다음과 같다.
$$h(x) = arg \max_{k \in \mathbf {Y}} \log P(y_k) + \sum^n_{j = 1} p(x_j | y_k)$$

---

데이터 분포(Data Distribution)에 따라 나이브 베이즈 분류기는 다음과 같이 종류가 나뉜다.

• 베르누이 나이브 베이즈 분류기(Bernoulli Naīve Bayes Classifier): 특징 $x_j$가 이진 값을 갖는다.
• 다항 분포 나이브 베이즈 분류기(Multinomial Naīve Bayes Classifier): 특징 $x_j$가 개수를 뜻한다.
• 가우시안 나이브 베이즈 분류기(Gaussian Naīve Bayes Classifier): 특징 $x_j$가 가우시안을 따르는 실수 값을 갖는다.

---

베르누이 나이브 베이즈 분류(Bernoulli Naīve Bayes Classification)

베르누이 나이브 베이즈 분류를 다음과 같은 예제로 이해해보자. 우선 다음과 같이 이진 특징(Binary Feature), 특징 벡터, 클래스 레이블, 학습 데이터세트를 표기한다고 가정하자. 

• 이진 특징 $x_j \in \mathbf {X} = \{ 0, 1 \}$
• 특징 벡터 $\mathbf {x} = (x_1, \cdots, x_n) \in \mathbf {X}^n$
• 클래스 레이블 $y \in \{ 1, \cdots, c \} \in \mathbf {Y}$
• 학습 데이터 세트 $(\mathbf {x}_1, y_1), \cdots, (\mathbf {x}_m, y_m) \in \mathbf {X}^n \times \mathbf {Y}$
  
  

※ 필수 명제 및 이론 정리

베르누이 분포(Bernoulli Distribution):
$$p(x; p) = p^x \cdot (1 - p)^{(1 - x)} \text { for } x \in {0, 1}$$
$Pr(x = 1) = p = 1 - Pr(x = 0) = 1 - q$

※ 클래스 레이블 $y_k$이 주어졌을 때, $j$ 번째 특징 $x_j$의 성공 확률(Success Probability)을 $p_{kj} = P(x_j = 1 | y_k)$로 표기한다.
레이블 $y_k$이 주어졌을 때 $x_j$의 우도는 다음과 같다.
$$P(x_j | y_k) = p^{x_j}_{kj} \cdot (1 - p_{kj})^{(1 - x_j)}$$
레이블 $y_k$이 주어졌을 때 $\mathbf {x}$의 우도는 다음과 같다.
$$P(\mathbf {x}| y_k) = \prod^n_{j = 1} p^{x_j}_{kj} \cdot (1 - p_{kj})^{(1 - x_j)}$$
따라서, 베르누이 나이브 베이즈 분류기는 다음과 같다.
$$h(x) = arg \max_{k \in \mathcal {Y}} P(y_k) \prod^n_{j = 1} p^{x_j}_{kj} \cdot (1 - p_{kj})^{(1 - x_j)}$$
로그를 취하면 베르누이 나이브 베이즈 분류는 선형 분류임을 증명할 수 있다.
$$\begin {align*}
h(x) &= arg \max_{k \in \mathcal {Y}} \log P(y_k) \sum^n_{j = 1} \log \left ( p^{x_j}_{kj} \cdot (1 - p_{kj})^{(1 - x_j)}  \right ) \\
&= arg \max_{k \in \mathcal {Y}} \log P(y_k) \sum^n_{j = 1} \left ( x_j \underbrace{\log p_{kj}}_{a_{kj}} + (1 - x_j) \underbrace {\log (1 - p_{kj})}_{b_{kj}}  \right ) \\
&= arg \max_{k \in \mathcal {Y}} \log P(y_k) + x^{\top} a_{k} + (1 - x)^{\top} b_{k} \\
&= arg \max_{k \in \mathcal {Y}} \log P(y_k) + x^{\top} (a_k - b_k) + 1^{\top} b_{k}
\end {align*}$$

---

추정값을 이용한 베르누이 나이브 베이즈 분류

베르누이 나이브 베이즈 분류기는 사전 확률(Prior Probability) $P(y_k)$과 우도 $p_{kj}$의 값을 구해야 계산할 수 있는데, 이는 실생활에서 한정된 데이터 양으로 정확한 확률 값들을 구하기가 어렵다. 따라서 사전 확률과 우도의 실제값이 아닌 주어진 데이터로 계산할 수 있는 추정량을 대신 사용한다.

사전 확률 $P(y_k)$의 추정치

$y_k$로 분류된 학습 예제의 개수를 총 학습 예제의 개수로 나누어 사전 확률 추정량을 구한다.
$$\hat {\pi}_k = \frac {\sum^m_{i = 1} \mathbb {I} \{ y_i = k \}}{m} = \frac {m_k}{m}$$

---

예 1) 라그랑주 승수법(Lagrange Multiplier)을 이용한 사전 확률 예측

---

우도 $p_{kj}$의 추정치

클래스 $y_k$에 분류된 특징 $x_j$ 중 그 값이 1인 ($x_j = 1$) 학습 예제의 개수를 $y_k$로 분류된 학습 예제의 개수로 나누어 우도 추정량을 구한다.
$$\hat {p}_{kj} = \frac {\sum^m_{i = 1} \mathbb {I} \{ y_i = k \} x_{ij}}{\sum^m_{i = 1} \mathbb {I} \{ y_i = k \}} = \frac {m_{kj}}{m_k}$$
추정값들을 이용해서 다음과 같이 $\mathbf {x}$가 속해야 할 클래스를 예측할 수 있다.
$$\begin {align*}
h(x) &= arg \max_{k \in \mathcal {Y}} P(y_k) \prod^n_{j = 1} p^{x_j}_{kj} \cdot (1 - p_{kj})^{(1 - x_j)} \\
\therefore \hat {y} &\in arg \max^c_{k = 1} \frac {m_k}{m} \prod^n_{j = 1} \left (\frac {m_{kj}}{m_k} \right )^{x_j} \left ( 1 - \frac {m_{kj}}{m_k}  \right )^{1 - x_j}
\end {align*}$$

---

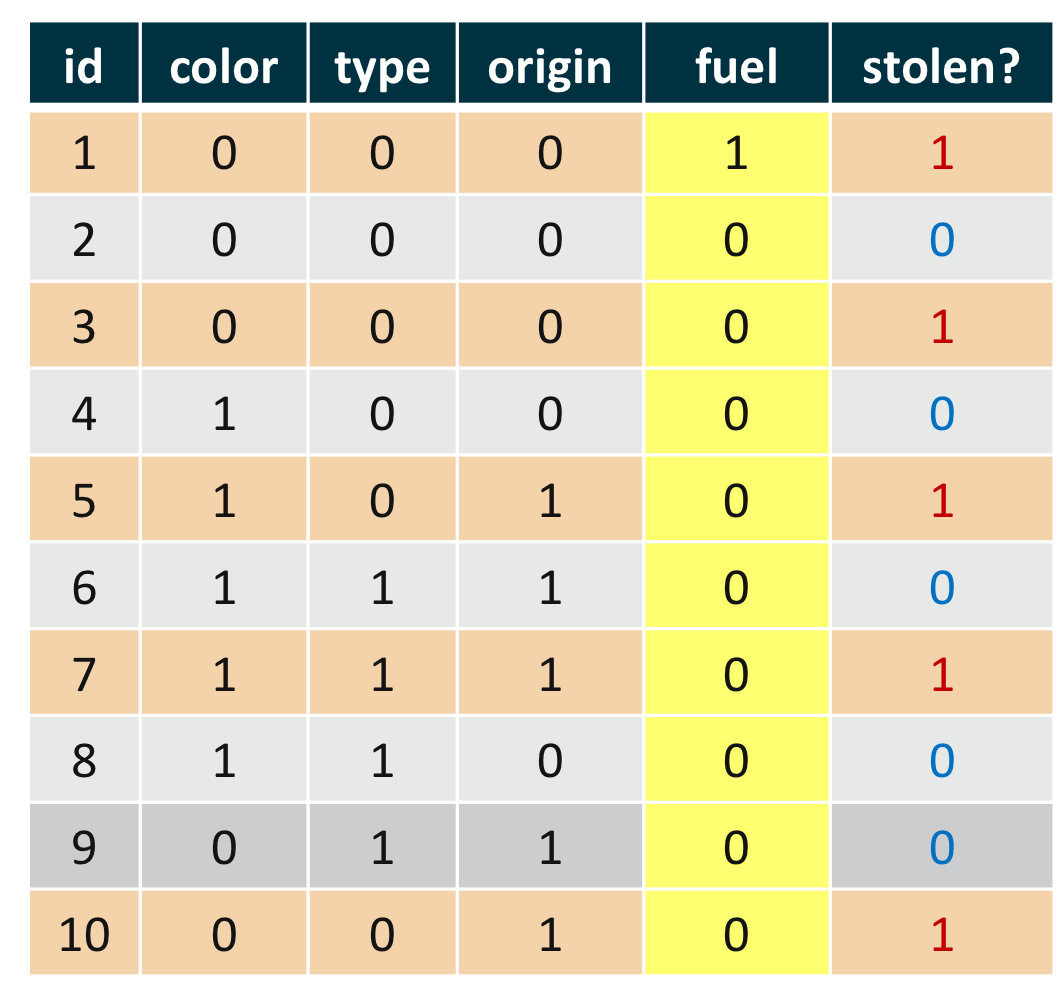
예제 1) 나이브 베이즈 분류의 예제

예를 들어, 오른쪽 표와 같은 학습 예제를 가정하자. 이를 베르누이 나이브 베이즈를 이용해 새로운 데이터 $\mathbf {x} = (0, 1, 0, 1)$을 분류하려면 우선 사전 확률과 우도의 추정치가 필요하다. 
사전 확률의 추정치는 다음과 같다. 총 학습 예제의 수는 0, 그중 각각 클래스 0으로 분류된 예제는 5개, 클래스 1로 분류된 예제도 5개이다.
$$\hat {P} (y_0) = \frac {5}{10} = 0.5$$
$$\hat {P} (y_1) = \frac {5}{10} = 0.5$$
클래스 0으로 분류된 예제 5개 중 color의 값이 1인 예제는 3개이므로 우도는 $\hat {p}_{01} = \frac {3}{5} = 0.6$이다. 마찬가지로 클래스 1로 분류된 예제 5개 중 color의 값이 1인 예제는 2개이므로 우도는 $\hat {p}_{11} = \frac {2}{5} = 0.4$이다. 모든 우도를 구하면 다음과 같다.
$$\begin {align*}
\hat {p}_{01} &= \frac {3}{5} = 0.6 & \hat {p}_{11} &= \frac {2}{5} = 0.4 \\
\hat {p}_{02} &= \frac {3}{5} = 0.6 & \hat {p}_{12} &= \frac {1}{5} = 0.2 \\
\hat {p}_{03} &= \frac {2}{5} = 0.4 & \hat {p}_{13} &= \frac {3}{5} = 0.6 \\
\hat {p}_{04} &= \frac {0}{5} = 0.0 & \hat {p}_{14} &= \frac {1}{5} = 0.2 \\
\end {align*}$$
$\mathbf {x} = (0, 1, 0, 1)$를 분류하려면 다음의 식들의 대소를 구해야 한다.
$$\begin {split}
h_0 (\mathbf {x}) &= \hat {P}(y_0) \prod^4_{j = 1} \hat {p}^{x_j}_{0j} \cdot (1 - \hat {p}_{0j})^{(1 - x_j)} \\
&= 0.5 \cdot (0.6^{0} \cdot (1 - 0.6)^{1 - 0}) \cdot (0.6^{1} \cdot (1 - 0.6)^{1 - 1}) \cdot (0.4^{0} \cdot (1 - 0.4)^{1 - 0}) \cdot (0^{1} \cdot (1 - 0)^{1 - 1}) \\
&= 0.5 \cdot 0.4 \cdot 0.6 \cdot 0.6 \cdot 0 \\
&= 0
\end {split}$$
$$\begin {split}
h_1 (\mathbf {x}) &= \hat {P}(y_1) \prod^4_{j = 1} \hat {p}^{x_j}_{1j} \cdot (1 - \hat {p}_{1j})^{(1 - x_j)} \\
&= 0.5 \cdot (0.4^{0} \cdot (1 - 0.4)^{1 - 0}) \cdot (0.2^{1} \cdot (1 - 0.2)^{1 - 1}) \cdot (0.6^{0} \cdot (1 - 0.6)^{1 - 0}) \cdot (0.2^{1} \cdot (1 - 0.2)^{1 - 1}) \\
&= 0.5 \cdot 0.6 \cdot 0.2 \cdot 0.4 \cdot 0.2 \\
&> 0
\end {split}$$
$$\therefore h_0 (\mathbf {x}) < h_1 (\mathbf {x})$$
따라서 $\mathbf {x} = (0, 1, 0, 1)$는 클래스 1로 분류한다.

---

라플라스 스무딩(Laplace Smoothing)

머신 러닝에서는 주로 한정된 양의 데이터가 주어지는데, 관찰된 값 중에 특히 특징의 값이 0일 때가 있다. 학습을 할 때, 통계학적 수치들로 모델을 구성하며, 한정된 데이터에서 관찰된 0 값들은 현실적인 통계 값을 계산하는데, 방해가 된다. 이런 문제를 제로 확률 문제(Zero Probability Problem)이라고 한다. 라플라스 스무딩은 이에 대한 해결 방안 중 하나며, 추정치를 구할 때 임의의 새로운 모수 $\alpha$를 각 항에 더해줘서 추정치들이 값 0에 덜 영향을 받도록 해준다.
$$\hat {p}_{kj} = \frac {m_{kj} + \alpha}{m_k + \alpha n}$$
$\alpha$를 0과 1 사이의 상수 값으로 설정해 우도를 계산하면 우도가 0이 되는 것을 방지한다.

---

다항 분포 나이브 베이즈 분류(Multinomial Naīve Bayes Classification)

다항 분포(Multinomial Distribution):
다항 분포는 여러 개의 값을 가질 수 있는 독립 확률변수들에 대한 확률 분포로, $M$번의 독립적 시행에서 각 $n$개의 사건 $e_1, \cdots, e_n$이 특정 횟수 $x_j$가 나타날 확률 $p_j$을 정의한다.
$$P(x) = \frac {(x_1 + \cdots + x_n)!}{x_1! \cdots x_n!} \cdot p_1^{x_1} \cdots p_n^{x_n}$$

※ 예를 들어, 총 100개의 공이 각각 3개의 다른 색깔로 구성될 때, 빨강색 공이 50개, 노란색 공이 30개, 초록색 공이 20개라고 하자. 6개의 공을 중복 조합을 할 때, 빨강색 공 3개, 노란색 공 2개, 초록색 공 1개를 뽑을 확률은 $P(x) = \frac {(3 + 2 + 1)!}{3! 2! 1!} \cdot 0.5^3 \cdot 0.3^2 \cdot 0.2^1 = 0.0225$이다.
레이블 $y_k$이 주어졌을 때 $\mathbf {x}$의 우도는 다음과 같다.
$$P(\mathbf {x}| y_k) = \underbrace{\frac {\left ( \sum^n_{j = 1} x_j \right )!}{\prod^n_{j = 1} x_j!}}_{\text{constant}} \prod^n_{j = 1} p^{x_j}_{kj}$$
다항 분포 나이브 베이즈 분류기는 다음과 같다.
$$h(x) = arg \max_{k \in \mathcal {Y}} P(y_k) \prod^n_{j = 1} p^{x_j}_{kj}$$

---

추정값을 이용한 다항 분포 나이브 베이즈 분류

사전 확률 $P(y_k)$의 추정치

$y_k$로 분류된 학습 예제의 개수를 총 학습 예제의 개수로 나누어 사전 확률 추정량을 구한다. 나이브 베이즈 종류와 상관없이 사전 확률의 추정치를 구하는 방법은 같다.
$$\hat {\pi}_k = \frac {\sum^m_{i = 1} \mathbb {I} \{ y_i = k \}}{m} = \frac {m_k}{m}$$

우도 $p_{kj}$의 추정치

클래스 $y_k$에 분류된 예제 중 사건 $e_j$가 발생하는 횟수를 $y_k$로 분류된 모든 사건의 발생 횟수로 나누어 우도 추정량을 구한다.
$$\hat {p}_{kj} = \frac {\sum^m_{i = 1} \mathbb {I} \{ y_i = k\}x_{ij}}{\sum^m_{i = 1} \sum^n_{j = 1} \mathbb {I} \{ y_i = k\} x_{ij}} = \frac {n_{kj}}{n_k}$$
라플라스 스무딩을 적용하면, $\hat {p}_{kj} = \frac {n_{kj} + \alpha }{n_k + \alpha n}$다.
추정값들을 이용해서 다음과 같이 $\mathbf {x}$가 속해야 할 클래스를 예측할 수 있다.
$$\begin {align*}
h(x) &= arg \max_{k \in \mathcal {Y}} P(y_k) \prod^n_{j = 1} p^{x_j}_{kj} \\
\therefore \hat {y} &\in arg \max^c_{k = 1} \frac {m_k}{m} \prod^n_{j = 1} \left ( \frac {n_{kj} + \alpha }{n_k + \alpha n} \right )^{x_j}
\end {align*}$$
※ 베르누이 나이브 베이즈 분류는 사건의 존재와 부재를 모델링하는 반면, 다항 분포 나이브 베이즈 분류는 사건의 존재만을 모델링한다.

---

가우시안 나이브 베이즈 분류(Gaussian Naīve Bayes Classification)

가우시안 분포(Gaussian Distribution):
평균이 $\mu$이고 분산이 $\sigma^2$일 때,
$$\mathcal {N} (\mu, \sigma^2) = \frac {1}{\sqrt {2 \pi} \sigma} \exp \left ( - \frac {1}{2} \left ( \frac {x - \mu}{\sigma} \right )^2 \right )$$

레이블 $y_k$이 주어졌을 때 $x_j$의 우도는 다음과 같다.
$$p(\mathbf {x}| y_k) = \mathcal {N} (\mu_{kj}, \sigma^2_{kj})$$
가우시안 나이브 베이즈 분류기는 다음과 같다.
$$h(x) = arg \max_{k \in \mathcal {Y}} P(y_k) \prod^n_{j = 1} \mathcal {N} (\mu_{kj}, \sigma^2_{kj})$$

---

추정값을 이용한 가우시안 나이브 베이즈 분류

사전 확률 $P(y_k)$의 추정치

$y_k$로 분류된 학습 예제의 개수를 총 학습 예제의 개수로 나누어 사전 확률 추정량을 구한다. 나이브 베이즈 종류와 상관없이 사전 확률의 추정치를 구하는 방법은 같다.
$$\hat {\pi}_k = \frac {\sum^m_{i = 1} \mathbb {I} \{ y_i = k \}}{m} = \frac {m_k}{m}$$

우도 $p_{kj}$의 추정치

$$\begin {align*}
m_k &= \sum^m_{i = 1} \mathbb {I} \{ y_i = k \} \\
\hat {\mu}_{kj} &= \frac {1}{m_k} \sum^m_{i = 1} \mathbb {I} \{ y_i = k \} x_{ij} \\
\hat {\sigma}^2_{kj} &= \frac {1}{m_k} \sum^m_{i = 1} \mathbb {I} \{ y_i = k \} (x_{ij} - \hat {\mu}_{kj})^2 \\
\end {align*}$$
추정값들을 이용해서 다음과 같이 $\mathbf {x}$가 속해야 할 클래스를 예측할 수 있다.
$$\begin {align*}
h(x) &= arg \max_{k \in \mathcal {Y}} P(y_k) \prod^n_{j = 1} \mathcal {N} (\mu_{kj}, \sigma^2_{kj}) \\
\therefore \hat {y} &\in arg \max^c_{k = 1} \hat {\pi}_k \prod^n_{j = 1} \mathcal {N} (\hat{\mu}_{kj}, \hat {\sigma}^2_{kj})
\end {align*}$$

---

나이브 베이즈 분류의 분석

나이브 베이즈 분류는 모든 특징들이 독립적이라는 가정 하에 모수의 개수를 대폭적으로 줄여 베이즈 분류의 계산의 어려움(Intractability)을 보완한다. 데이터 분포에 따라 나이브 베이즈 분류가 여러 종류 모델로 나뉘는데, 모든 모델이 학습과 예측을 빠르게 수행할 수 있고, 작동 원리 또한 쉽게 이해 및 해석이 가능하다. 또 다른 장점으로서, 설정해야 할 초모수(Hyperparameter)가 상대적으로 적다는 점도 있다. 단, 단점으로는 학습을 시작하기 전에 데이터 분포를 먼저 추정해야 한다.

---

 참조

1. Richard O. Duda, Peter E. Hart, and David G. Stork. 2000. Pattern Classification (2nd Edition). Wiley-Interscience, USA.
2. Müller, K.R., Montavon, G. (2021). Lecture on Machine Learning 1-X. Technische Universität Berlin, Berlin, Germany.
3. Lommatzsch, A. (2021). Lecture on Foundations of Data Science. Technische Universität Berlin, Berlin, Germany.